题目内容
16.(1)化简:($\frac{1}{3}$x+$\frac{3}{4}$y)($\frac{1}{3}$x-$\frac{3}{4}$y)-($\frac{1}{3}$x-$\frac{3}{4}$y)(2)先化简,在求值:(4ab3-8a2b2)÷4ab+(2a+b)(2a-b),其中a=2,b=1.
分析 (1)根据平方差公式进行化简运算即可.
(2)根据整式乘除法则即可化简求值.
解答 解:(1)原式=$\frac{1}{9}$x2-$\frac{9}{16}$y2-$\frac{1}{3}$x+$\frac{3}{4}$y
(2)当a=2,b=1时,
原式=b2-2ab+4a2-b2
=4a2-2ab
=4×4-2×2×1
=16-4
=12
点评 本题考查整式化简运算,解题的关键是熟练运用整式运算的法则,本题属于基础题型.

练习册系列答案
相关题目
1.有一人患了流感,经过两轮传染后共有111人患了流感,每轮传染中平均一个人传染的人数为( )
| A. | 12 | B. | 11 | C. | 10 | D. | 9 |
8.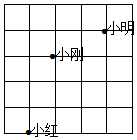 如图所示是做课间操时,小明、小红、小刚三人的相对位置,如果用(4,5)表示小明的位置,(2,4)表示小刚的位置,则小红的位置可表示为( )
如图所示是做课间操时,小明、小红、小刚三人的相对位置,如果用(4,5)表示小明的位置,(2,4)表示小刚的位置,则小红的位置可表示为( )
 如图所示是做课间操时,小明、小红、小刚三人的相对位置,如果用(4,5)表示小明的位置,(2,4)表示小刚的位置,则小红的位置可表示为( )
如图所示是做课间操时,小明、小红、小刚三人的相对位置,如果用(4,5)表示小明的位置,(2,4)表示小刚的位置,则小红的位置可表示为( )| A. | (0,0) | B. | (0,1) | C. | (1,0) | D. | (1,1) |
5.某超市在“十一”期间对顾客实行优惠购物的条款如下表:
(1)甲顾客一次性购物800元,他实际付款690元.
(2)乙顾客在该超市一次性购物x元,当200≤x<500时,他实际付款0.9x元;当x≥500时,他实际付款(0.8x+50)元;(用含x的代数式表示)
(3)丙顾客两次购物货款合计为820元,第一次购物的货款为a元(200<a<300),试用a的代数式表示丙顾客两次购物实际付款合计多少元?
| 一次性购物 | 优惠办法 |
| 少于200元 | 不予优惠 |
| 低于500元但不低于200元 | 九折优惠 |
| 500元或超过500元 | 其中500元部分给予九折优惠; 超过500元部分给予八折优惠 |
(2)乙顾客在该超市一次性购物x元,当200≤x<500时,他实际付款0.9x元;当x≥500时,他实际付款(0.8x+50)元;(用含x的代数式表示)
(3)丙顾客两次购物货款合计为820元,第一次购物的货款为a元(200<a<300),试用a的代数式表示丙顾客两次购物实际付款合计多少元?
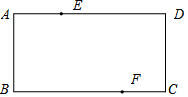 如图,已知矩形ABCD,分别在边AD,BC上找一点E和F,使四边形DEBF是菱形.
如图,已知矩形ABCD,分别在边AD,BC上找一点E和F,使四边形DEBF是菱形.