题目内容
AD是△ABC的边BC上的中线,AB=14,AC=6,则边BC的取值范围是 ;中线AD的取值范围是 .
考点:全等三角形的判定与性质,三角形三边关系
专题:
分析:根据三角形的三边关系定理求出BC的范围即可;延长AD到E,使AD=DE,连接BE,证三角形全等,推出BE=AC=6,在三角形ABE中,根据三角形的三边关系定理求出即可.
解答:解:∵在△ABC中,AB=14,AC=6,
∴14-6<BC<14+6,
∴8<BC<20;

延长AD到E,使AD=DE,连接BE,
∵AD为中线,
∴BD=DC,
在△ADC和△EDB中
∴△ADC≌△EDB,
∴AC=BE=6,
在△ABE中,AB=14,BE=6,
∴14-6<AE<14+6,
∴8<2AD<20,
∴4<AD<10,
故答案为:8<BC<20,4<AD<10.
∴14-6<BC<14+6,
∴8<BC<20;

延长AD到E,使AD=DE,连接BE,
∵AD为中线,
∴BD=DC,
在△ADC和△EDB中
|
∴△ADC≌△EDB,
∴AC=BE=6,
在△ABE中,AB=14,BE=6,
∴14-6<AE<14+6,
∴8<2AD<20,
∴4<AD<10,
故答案为:8<BC<20,4<AD<10.
点评:本题考查了全等三角形的性质和判定,三角形的三边关系定理的应用,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应边相等,对应角相等.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
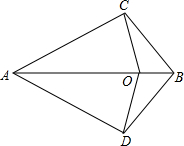 已知,如图,AC=AD,BC=BD,O为AB上一点,
已知,如图,AC=AD,BC=BD,O为AB上一点,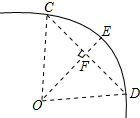 如图,一条公路的转弯处是一段圆弦(即图中
如图,一条公路的转弯处是一段圆弦(即图中
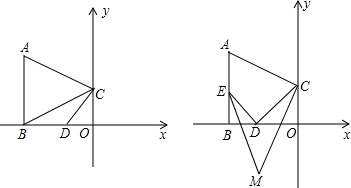
 如图,AB是圆O的直径,C是圆O上一点,∠CAB=30°,延长AB到D,使BD=BO,求证:DC是圆O的切线.
如图,AB是圆O的直径,C是圆O上一点,∠CAB=30°,延长AB到D,使BD=BO,求证:DC是圆O的切线.