题目内容
已知关于x的一元二次方程(a2+1)x2-2(a+b)x+b2+1=0.
(1)当b=2时,方程有一个实数根为2,求a的取值范围;
(2)若此方程有实数根,当2<a<6时,求b的取值范围.
(1)当b=2时,方程有一个实数根为2,求a的取值范围;
(2)若此方程有实数根,当2<a<6时,求b的取值范围.
考点:根的判别式,根与系数的关系
专题:
分析:(1)把x=2,b=2代入方程得出4(a2+1)-4(a+2)+5=4a2-4a+1=0,解方程求得a的值即可;
(2)根据根的判别式得出△=4(a+b)2-4(a2+1)(b2+1)≥0,进一步整理得出a、b的关系,代换求得b的取值范围即可.
(2)根据根的判别式得出△=4(a+b)2-4(a2+1)(b2+1)≥0,进一步整理得出a、b的关系,代换求得b的取值范围即可.
解答:解:(1)把b=2,x=2代入方程得4(a2+1)-4(a+2)+4+1=0,
解得a1=a2=
,
即a的值为
;
(2)根据题意得△=4(a+b)2-4(a2+1)(b2+1)≥0,
∴(ab)2-2ab+1≤0,即(ab-1)2≤0,
∴ab-1=0,
∴a=
,
∵2<a<6,
∴
<b<
.
解得a1=a2=
| 1 |
| 2 |
即a的值为
| 1 |
| 2 |
(2)根据题意得△=4(a+b)2-4(a2+1)(b2+1)≥0,
∴(ab)2-2ab+1≤0,即(ab-1)2≤0,
∴ab-1=0,
∴a=
| 1 |
| b |
∵2<a<6,
∴
| 1 |
| 6 |
| 1 |
| 2 |
点评:此题主要考查一元二次方程的解法,一元二次方程根的判别式,理解和掌握基础知识是解决问题的关键.

练习册系列答案
相关题目
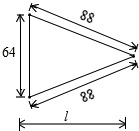 已知一个工件尺寸如图(单位:mm),计算l的长(精确到1mm).
已知一个工件尺寸如图(单位:mm),计算l的长(精确到1mm). 如图,某装置有一枚指针,原来指向南偏西50°,把这枚指针按顺时针方向旋转90°.
如图,某装置有一枚指针,原来指向南偏西50°,把这枚指针按顺时针方向旋转90°.