题目内容
14.抛物线y=-$\frac{1}{2}$x2+(6-m)x+m-3与x轴交于A,B两点,且A,B两点关于y轴对称.(1)求m的值;
(2)求抛物线的解析式及顶点的坐标.
分析 (1)根据题意,可知对称轴为y轴,根据对称轴的公式求出m的值即可;
(2)根据第(1)小题的m的值,求出抛物线的解析式,根据解析式,利用顶点坐标公式,求出顶点坐标即可.
解答 解:(1)∵抛物线y=$-\frac{1}{2}{x}^{2}$+(6-m)x+m-3与x轴交于点A、B两点,且A、B两点关于y轴对称,
∴$-\frac{b}{2a}=-\frac{6-m}{2×(-\frac{1}{2})}=6-m=0$,解得:m=6,
(2)由(1)可知,抛物线解析式为:$y=-\frac{1}{2}{x}^{2}+3$,
∴$-\frac{b}{2a}=-\frac{0}{2×(-\frac{1}{2})}=0$,$\frac{4ac-{b}^{2}}{4a}=\frac{4×(-\frac{1}{2})×3-0}{4×(-\frac{1}{2})}=3$,
∴顶点坐标为(0,3).
点评 本题主要考查抛物线与x轴的交点、抛物线顶点坐标公式,解决第(1)小题的关键是明确对称轴是y轴,第(2)小题的关键是熟记顶点公式.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
5.在等式6a2•(-b3)2÷( )2=$\frac{2}{3}$中的括号内应填入( )
| A. | $\frac{1}{9}{a}^{2}{b}^{6}$ | B. | $\frac{1}{3}a{b}^{3}$ | C. | ±$\frac{1}{3}a{b}^{3}$ | D. | ±3ab3 |
9.将一些数排列查过下表:
观察规律后完成下列问题:
(1)第10行第2列的数是40;
(2)数81在9行1列;
(3)第n行第1列的数是n2;
(4)请写出数100所在的行和列.
| 第1列 | 第2列 | 第3列 | 第4列 | |
| 第1行 | 1 | 4 | 5 | 10 |
| 第2行 | 4 | 8 | 10 | 12 |
| 第3行 | 9 | 12 | 15 | 14 |
| … | … | … | … | … |
(1)第10行第2列的数是40;
(2)数81在9行1列;
(3)第n行第1列的数是n2;
(4)请写出数100所在的行和列.
6.已知代数式x+3y的值是2,则代数式2x+6y+1的值是( )
| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
 如图是边长为a的正方形工件,四角各打了一个半径为r的圆孔,用代数式表示阴影部分的面积是a2-4πr2.
如图是边长为a的正方形工件,四角各打了一个半径为r的圆孔,用代数式表示阴影部分的面积是a2-4πr2.
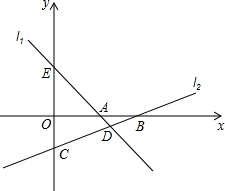 如图,直线l1:y=-x+3与x轴相交于点A,与y轴交于点E.直线l2:y=kx+b经过点(3,-1),与x轴交于点B(6,0),与y轴交于点C,与直线l1相交于点D.
如图,直线l1:y=-x+3与x轴相交于点A,与y轴交于点E.直线l2:y=kx+b经过点(3,-1),与x轴交于点B(6,0),与y轴交于点C,与直线l1相交于点D.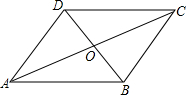 如图,平行四边形ABCD中,AC=12,BD=10,AB=m,则m的取值范围为1<x<11.
如图,平行四边形ABCD中,AC=12,BD=10,AB=m,则m的取值范围为1<x<11.