题目内容
19.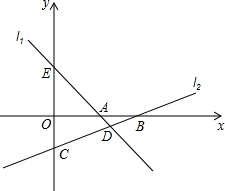 如图,直线l1:y=-x+3与x轴相交于点A,与y轴交于点E.直线l2:y=kx+b经过点(3,-1),与x轴交于点B(6,0),与y轴交于点C,与直线l1相交于点D.
如图,直线l1:y=-x+3与x轴相交于点A,与y轴交于点E.直线l2:y=kx+b经过点(3,-1),与x轴交于点B(6,0),与y轴交于点C,与直线l1相交于点D.(1)求直线l2的函数关系式;
(2)点P是l2上一点,若△ABP的面积等于△ABD的面积的2倍,求点P的坐标;
(3)设点Q的坐标为(m,3),是否存在m的值使得QA+QB最小?若存在,请求出点Q的坐标;若不存在,请说明理由;
(4)动点M从A出发,沿点A向点E运动,运动速速为每秒1个单位长度,点M运动到点E时停止运动,当运动2$\sqrt{2}$秒时,在坐标轴上是否存在点T使得△AMT是以AM为直角边的直角三角形?若存在,请直接写出点T的坐标;若不存在,请说明理由.
分析 (1)设直线l2的解析式为y=kx+b(k≠0),把点(3,-1),B(6,0)代入求出k,b的值即可得出结论;
(2)设P(x,$\frac{1}{3}$x-2),联立两直线的解析式可得出D点坐标,再由△ABP的面积等于△ABD的面积的2倍可得出结论;
(3)先求出A、E两点的坐标,过点E作直线EM∥x轴,作点A关于直线EM的对称点A′,连接A′B交直线EM于点Q,则点Q即为所求点,利用待定系数法求出直线A′B的解析式,进而可得出Q点的坐标.
(4)根据勾股定理求出AE的长,过点M作MG⊥x轴于点G,由相似三角形的性质求出M点的坐标,再分∠MAT=90°与∠AMT=90°两种情况进行讨论.
解答 解:(1)设直线l2的解析式为y=kx+b(k≠0),
∵点(3,-1),B(6,0),
∴$\left\{\begin{array}{l}3k+b=-1\\ 6k+b=0\end{array}\right.$,解得$\left\{\begin{array}{l}k=\frac{1}{3}\\ b=-2\end{array}\right.$.
∴直线l2的解析式为y=$\frac{1}{3}$x-2;
(2)设P(x,$\frac{1}{3}$x-2),
∵$\left\{\begin{array}{l}y=-x+3\\ y=\frac{1}{3}x-2\end{array}\right.$,
∴D($\frac{15}{4}$,-$\frac{3}{4}$).
∵△ABP的面积等于△ABD的面积的2倍,
∴|$\frac{1}{3}$x-2|=2×$\frac{3}{4}$,解得x=$\frac{3}{2}$或$\frac{21}{2}$.
∴P($\frac{3}{2}$,-$\frac{3}{2}$)或($\frac{21}{2}$,$\frac{3}{2}$);
(3)存在.
∵直线y=-x+3与x轴相交于点A,与y轴交于点E,
∴A(3,0),E(0,3).
过点E作直线EM∥x轴,作点A关于直线EM的对称点A′,则A′(3,6),
设直线A′B的解析式为y=ax+c(a≠0),
∵B(6,0),
∴$\left\{\begin{array}{l}6a+c=0\\ 3a+c=6\end{array}\right.$,解得$\left\{\begin{array}{l}a=-2\\ c=12\end{array}\right.$.
∴直线A′B的解析式为y=-2x+12,
∴当y=3时,x=$\frac{9}{2}$,
∴Q($\frac{9}{2}$,3);
(4)存在.
∵如图2,A(3,0),E(0,3),
∴AE=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$.
过点M作MG⊥x轴于点G,则△AMG∽△AEO,
∴$\frac{AG}{OA}$=$\frac{AM}{AE}$,即$\frac{AG}{3}$=$\frac{2\sqrt{2}}{3\sqrt{2}}$,解得AG=AG=2,
∴M(1,2).
设直线AT的解析式为y=x+b,
当∠MAT=90°时,∵A(3,0),
∴3+b=0,解得b=-3,
∴直线AT的解析式为y=x-3,
∴当x=0时,y=-3,即T1(0,-3);
当∠AMT=90°时,
∵M(1,2),
∴1+b=2,解得b=1,
∴直线AT的解析式为y=x+1,
∴当x=0时,y=1;当y=0时x=-1,
∴T2(0,1),T3(-1,0).
综上所示,T点坐标为T1(0,-3),T2(0,1),T3(-1,0).
点评 本题考查的是一次函数综合题,涉及到一次函数图象上点的坐标特点、轴对称-最短路线问题、相似三角形的判定与性质等知识,在解答(4)时要注意进行分类讨论,不要漏解.

 阅读快车系列答案
阅读快车系列答案| A. | 0 | B. | -1 | C. | -9 | D. | 1 |
 如图,以BC为边的三角形有( )个.
如图,以BC为边的三角形有( )个.| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
| A. | 正整数、负整数统称为整数 | B. | 3.14不是有理数 | ||
| C. | 0是最小的有理数 | D. | 2.4是分数 |
| A. | 8 | B. | 3π | C. | 5$\sqrt{5}$ | D. | 5$\sqrt{3}$ |