题目内容
 如图,点A在反比例函数y=
如图,点A在反比例函数y=| 4 |
| x |
| 9 |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:反比例函数图象上点的坐标特征,相似三角形的判定与性质
专题:
分析:首先过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,易得△OBD∽△AOC,又由点A在反比例函数y=
的图象上,点B在反比例函数y=-
的图象上,即可得S△OBD=4.5,S△AOC=2,然后根据相似三角形面积的比等于相似比的平方,即可得
=
,然后由正切函数的定义求得答案.
| 4 |
| x |
| 9 |
| x |
| OB |
| OA |
| 3 |
| 2 |
解答: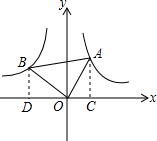 解:过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,
解:过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,
∴∠ACO=∠ODB=90°,
∴∠OBD+∠BOD=90°,
∵∠AOB=90°,
∴∠BOD+∠AOC=90°,
∴∠OBD=∠AOC,
∴△OBD∽△AOC,
∴
=(
)2,
∵点A在反比例函数y=
的图象上,点B在反比例函数y=-
的图象上,
∴S△OBD=4.5,S△AOC=2,
∴
=
,
∴tan∠OAB=
=
.
故选C.
 解:过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,
解:过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,∴∠ACO=∠ODB=90°,
∴∠OBD+∠BOD=90°,
∵∠AOB=90°,
∴∠BOD+∠AOC=90°,
∴∠OBD=∠AOC,
∴△OBD∽△AOC,
∴
| S△OBD |
| S△AOC |
| OB |
| OA |
∵点A在反比例函数y=
| 4 |
| x |
| 9 |
| x |
∴S△OBD=4.5,S△AOC=2,
∴
| OB |
| OA |
| 3 |
| 2 |
∴tan∠OAB=
| OB |
| OA |
| 3 |
| 2 |
故选C.
点评:此题考查了相似三角形的判定与性质、反比例函数的性质以及直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用,注意掌握辅助线的作法.

练习册系列答案
相关题目
已知关于x的一元一次方程2x+3k=x-6的解是正数,则k的取值范围是( )
| A、k>2 | B、k>-2 |
| C、k<2 | D、k<-2 |
在物理学里面,光的速度约为8亿米/秒,该速度用科学记数法表示为( )
| A、0.8×108 |
| B、8×106 |
| C、8×108 |
| D、8×109 |
 如图,四边形ABCD是一个边长为10米的正方形,甲、乙两玩具车分别从A、B两地同时出发,都沿A→B→C→D→A→…的方向行走,甲车每分钟走6米,乙车每分钟走10米,则两玩具车第一次相遇时所处位置是在正方形的边( )
如图,四边形ABCD是一个边长为10米的正方形,甲、乙两玩具车分别从A、B两地同时出发,都沿A→B→C→D→A→…的方向行走,甲车每分钟走6米,乙车每分钟走10米,则两玩具车第一次相遇时所处位置是在正方形的边( )| A、AB上 | B、BC上 |
| C、CD上 | D、AD上 |
计算6tan60°-2cos30°的结果是( )
A、4
| ||
B、6
| ||
C、
| ||
D、5
|
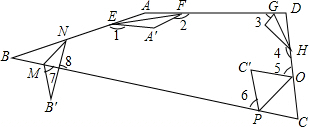 如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7-∠8的值是( )
如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7-∠8的值是( )| A、600° | B、700° |
| C、720° | D、800° |
代数式xy2-y2( )
| A、它是单项式 |
| B、它是x,y的积的平方与y平方的差 |
| C、它是三次二项式 |
| D、它的二次项系数为1 |
 如图:Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.
如图:Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.