题目内容
 如图,点P在正方形ABCD内,△PBC是正三角形,BD和PC相交于点E.给出下列结论:
如图,点P在正方形ABCD内,△PBC是正三角形,BD和PC相交于点E.给出下列结论:①∠PBD=15°;
②△PDE为等腰三角形;
③△PDE∽△PCD;
④△PBD、正方形ABCD的面积分别为S1,S,若S=4,则S1=1.
其中正确的是
考点:相似三角形的判定与性质,等腰三角形的判定,等边三角形的性质,正方形的性质
专题:
分析:根据等边三角形性质得出∠PCB=60°,PC=BC,∠PBC=60°,根据正方形性质和等腰三角形性质求出∠DBC=45°,即可判断①;
根据三角形内角和定理和三角形外角性质求出∠DPC=∠PDC=75°,即可判断②;
根据三角形相似的判定即可判断③;
根据三角形的面积求出△PBC,△DPC,△DBC的面积,即可判断④.
根据三角形内角和定理和三角形外角性质求出∠DPC=∠PDC=75°,即可判断②;
根据三角形相似的判定即可判断③;
根据三角形的面积求出△PBC,△DPC,△DBC的面积,即可判断④.
解答:解:∵△PBC是等边三角形,
∴∠PCB=60°,PC=BC,∠PBC=60°,
∵四边形ABCD是正方形,
∴BC=CD,∠DCB=90°,
∴∠DBC=45°,
∴∠PBD=60°-45°=15°,∴①正确;
∵∠DCB=90°,∠PCB=60°,
∴∠DCP=90°-60°=30°,
∵BC=PC,BC=CD,
∴PC=DC,
∴∠CPD=∠PDC=
(180°-30°)=75°,
∵∠DCP=30°,∠BDC=45°,
∴∠DEP=45°+30°=75°=∠DPC,
∴DP=DE,
∴△PDE为等腰三角形,∴②正确;
∵∠DPC=∠DPC,∠DEP=∠PDC=75°,
∴△PDE∽△DCP,∴③正确;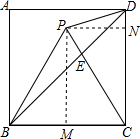
过P作PN⊥CD,PM⊥BC,
则∠PNC=∠PMC=90°,
∵正方形ABCD的面积是4,
∴BC=DC=2,
∵PC=BC,
∴PC=2,
∵∠DCP=30°,∠PNC=90°,
∴PN=
PC=1,PM=PC×sin60°=2×
=
,
∴S1=S△PBD
=S△PBC+S△PDC-S△DBC
=
×2×
+
×2×1-
×2×2=
-1,∴④错误;
故答案为:①②③.
∴∠PCB=60°,PC=BC,∠PBC=60°,
∵四边形ABCD是正方形,
∴BC=CD,∠DCB=90°,
∴∠DBC=45°,
∴∠PBD=60°-45°=15°,∴①正确;
∵∠DCB=90°,∠PCB=60°,
∴∠DCP=90°-60°=30°,
∵BC=PC,BC=CD,
∴PC=DC,
∴∠CPD=∠PDC=
| 1 |
| 2 |
∵∠DCP=30°,∠BDC=45°,
∴∠DEP=45°+30°=75°=∠DPC,
∴DP=DE,
∴△PDE为等腰三角形,∴②正确;
∵∠DPC=∠DPC,∠DEP=∠PDC=75°,
∴△PDE∽△DCP,∴③正确;

过P作PN⊥CD,PM⊥BC,
则∠PNC=∠PMC=90°,
∵正方形ABCD的面积是4,
∴BC=DC=2,
∵PC=BC,
∴PC=2,
∵∠DCP=30°,∠PNC=90°,
∴PN=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴S1=S△PBD
=S△PBC+S△PDC-S△DBC
=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
故答案为:①②③.
点评:本题考查了正方形性质,等边三角形的性质,含30度角的直角三角形,三角形面积,等腰三角形的性质,三角形的内角和定理,相似三角形的判定等知识点的应用,主要考查学生的推理能力,题目是一道中等题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知关于x的一元一次方程2x+3k=x-6的解是正数,则k的取值范围是( )
| A、k>2 | B、k>-2 |
| C、k<2 | D、k<-2 |
 如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE,若∠E=50°,则∠BAO的大小为
如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE,若∠E=50°,则∠BAO的大小为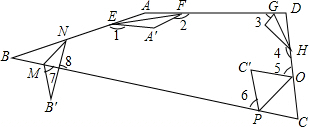 如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7-∠8的值是( )
如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7-∠8的值是( )