题目内容
4．
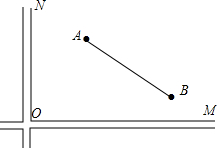如图，在两条相互垂直的高速公路0M、0N旁有两个相距50km的风景区A和B，A、B到0M的距离分别为40kn和10km，A到0N的距离为30km，现打算在0M旁和0N旁各修建一服务区C、D，使A、B、C、D构成的四边形的周长最小，求出这个最小值（高速公路的宽忽略不计）．
分析 过A作关于ON的对称点A'，过B作关于OM的对称点B'，连接A'B'，交ON于点D，交OM于点C，求出A'B'的值即可．
解答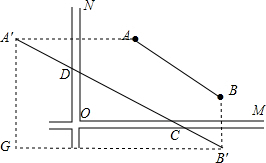 
解：过A作关于X轴的对称点A'，过B作关于OM的对称点B'，
连接A'B'，交OM于点C，交ON于点D，则C，D即为所求．
过A'、B'分别作ON、OM的平行线交于点G，
∵A、B到0M的距离分别为40kn和10km，A到0N的距离为30km，
∴B到0N的距离为40+30=70km，
∴A′G=40+10=50km，B′G=30+30+40=100km，
∴A′B′=$\sqrt{A′{G}^{2}+B′{G}^{2}}$=50$\sqrt{5}$，
∴这个最小值是（50$\sqrt{5}$+50）km..
点评 此题考查了线路最短的问题，确定动点为何位置是关键，综合运用勾股定理的知识．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
12．点A（-1，-2），点B（3，4），则线段AB与x轴正半轴夹角的正弦值为（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{\sqrt{5}}{5}$ | C． | $\frac{3\sqrt{13}}{13}$ | D． | $\frac{2\sqrt{13}}{13}$ |
19．
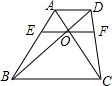如图，在梯形ABCD中，AD∥BC，AC，BD相交于点O，过点O作EF∥AD分别交AB，CD于点E、F．下列各式中不正确的是（ ）
如图，在梯形ABCD中，AD∥BC，AC，BD相交于点O，过点O作EF∥AD分别交AB，CD于点E、F．下列各式中不正确的是（ ）| A． | $\frac{AE}{EB}$=$\frac{DF}{FC}$ | B． | $\frac{OA}{OC}$=$\frac{OD}{OB}$ | C． | $\frac{AE}{AB}$=$\frac{DO}{BO}$ | D． | $\frac{CD}{CF}$=$\frac{BD}{BO}$ |