题目内容
6.如图①,平行四边形纸条ABCD中,E、F分别是AD、BC的中点,请观察从图①到图②的操作过程,并按要求解答下列问题.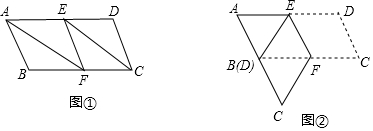
(1)在图①中,有多少个平行四边形(平行四边形ABCD除外),并选择其中一个给予证明;
(2)从图②中可看出,沿EF对折后,D与B重合,试问平行四边形ABCD除一般平行四边形所应有的性质外,它还具备有什么特有性质?(不必说明理由);
(3)在图②中,若再沿AF对折,要使点E与点B(或D)重合,那么平行四边形ABCD还应增加什么条件?请合情合理地说明之.
分析 (1)由平行四边形的性质得出AD=BC,AD∥BC,由中点的定义得出AE=DE=BF=CF,即可得出结论;
(2)由折叠的性质得:EF⊥BD,由平行四边形的性质得出AB∥EF∥CD,即可得出BD⊥CD,BD⊥AB;
(3)由折叠的性质得出AE=AB,由AD=2AE,即可得出AD=2AB.
解答 解:(1)有3个平行四边形(平行四边形ABCD除外),平行四边形ABFE、平行四边形CDEF、平行四边形AFCE;理由如下:
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵E、F分别是AD、BC的中点,
∴AE=DE=$\frac{1}{2}$AD,BF=CF=$\frac{1}{2}$BC,
∴AE=DE=BF=CF,
∴四边形ABFE、四边形CDEF、四边形AFCE是平行四边形;
(2)平行四边形ABCD还具备EF⊥BD,BD⊥CD,BD⊥AB的性质;理由如下:
∵沿EF对折后,D与B重合,
∴由折叠的性质得:EF⊥BD,
∵四边形ABFE、四边形CDEF是平行四边形,
∴AB∥EF∥CD,
∴BD⊥CD,BD⊥AB;
(3)还需要增加条件AD=2AB;理由如下:
∵沿AF对折,使点E与点B(或D)重合,即B与E关于AF对称,
则AE=AB,
∵AD=2AE,
∴AD=2AB.
点评 本题是四边形综合题目,考查了平行四边形的判定与性质、折叠的性质、中点的定义等知识;本题综合性强,熟练掌握平行四边形的判定与性质是解决问题的关键.

练习册系列答案
相关题目
16.在下列各式中,不成立的是( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{-2}$ | C. | -$\sqrt{{(-2)}^{2}}$ | D. | $\sqrt{-(-2)}$ |


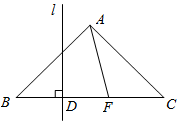 如图,等腰Rt△ABC中,∠BAC=90°,AB=AC=2,点F是边BC上不与点B,C重合的一个动点,直线l垂直平分BF,垂足为D,当△AFC是等腰三角形时,BD的长为$\frac{\sqrt{2}}{2}$或$\sqrt{2}$-1.
如图,等腰Rt△ABC中,∠BAC=90°,AB=AC=2,点F是边BC上不与点B,C重合的一个动点,直线l垂直平分BF,垂足为D,当△AFC是等腰三角形时,BD的长为$\frac{\sqrt{2}}{2}$或$\sqrt{2}$-1.