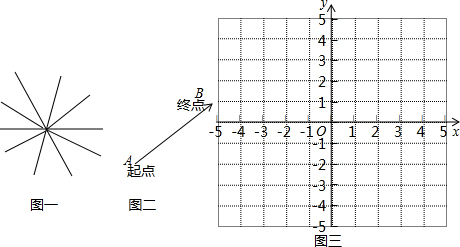
题目内容
 △ABC、△A1B1C1在平面直角坐标系位置如图(方格小正方形的边长为1)
△ABC、△A1B1C1在平面直角坐标系位置如图(方格小正方形的边长为1)(1)试说明△A1B1C1是由△ABC如何平移得到的;
(2)画出△A1B1C1绕O点旋转180°的△A2B2C2,点B2的坐标是
(3)点C1关于x轴对称点为C3,则△A1B1C3的面积
考点:作图-旋转变换,作图-平移变换
专题:作图题
分析:(1)根据对应点A、A1的平移规律写出即可;
(2)根据网格结构找出点A1、B1、C1绕O点旋转180°的A2、B2、C2的位置,然后顺次连接即可,再根据平面直角坐标系写出点B2的坐标即可;
(3)根据网格结构找出点C3的位置,然后根据三角形所在的矩形的面积减去四周三个三角形的面积,列式进行计算即可得解.
(2)根据网格结构找出点A1、B1、C1绕O点旋转180°的A2、B2、C2的位置,然后顺次连接即可,再根据平面直角坐标系写出点B2的坐标即可;
(3)根据网格结构找出点C3的位置,然后根据三角形所在的矩形的面积减去四周三个三角形的面积,列式进行计算即可得解.
解答: 解:(1)根据图形,△A1B1C1是由△ABC向右平移7个单位,向下平移2个单位得到;
解:(1)根据图形,△A1B1C1是由△ABC向右平移7个单位,向下平移2个单位得到;
(2)如图所示,△A2B2C2,即为所求作的三角形,点B2的坐标是(-5,-3);
(3)S△A1B1C3=3×2-
×1×3-
×1×2-
×1×2
=6-
-1-1
=
.
故答案为:(2)(-5,-3),(3)
.
 解:(1)根据图形,△A1B1C1是由△ABC向右平移7个单位,向下平移2个单位得到;
解:(1)根据图形,△A1B1C1是由△ABC向右平移7个单位,向下平移2个单位得到;(2)如图所示,△A2B2C2,即为所求作的三角形,点B2的坐标是(-5,-3);
(3)S△A1B1C3=3×2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=6-
| 3 |
| 2 |
=
| 5 |
| 2 |
故答案为:(2)(-5,-3),(3)
| 5 |
| 2 |
点评:本题考查了利用旋转变换,平移变换作图,准确找出对应点的位置是解题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
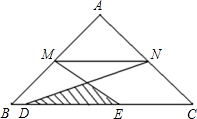 如图所示,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连接DN、EM,若AB=10cm,BC=16cm,DE=8cm,则图中阴影部分的面积为( )
如图所示,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连接DN、EM,若AB=10cm,BC=16cm,DE=8cm,则图中阴影部分的面积为( )| A、4cm2 |
| B、6cm2 |
| C、8cm2 |
| D、12cm2 |
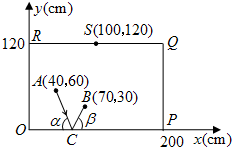 实验探究:下面设想用电脑模拟台球游戏,为简单起见,约定:①每个球或球袋都视为一点,如不遇障碍,各球均沿直线前进;②A球击中B球,意味着B球在A球前进的路线上,且B球被撞击后沿着A球原来的方向前进;③球撞及桌边后的反弹角等于入射角.
实验探究:下面设想用电脑模拟台球游戏,为简单起见,约定:①每个球或球袋都视为一点,如不遇障碍,各球均沿直线前进;②A球击中B球,意味着B球在A球前进的路线上,且B球被撞击后沿着A球原来的方向前进;③球撞及桌边后的反弹角等于入射角.