题目内容
小聪想利用树影测量树高,他在某时刻得小树的高为1.2m,树影的长为0.8m,但当他马上测得大树影时,因该大树在坡角为30°的斜坡附近,影子一部分落在水平地面上,一部分落在30度的斜坡上,他先测得水平地面上的影AB为3.4m,又测得斜坡上的影BC的长为2.8m,请你帮小聪测出树AD的高(精确到0.1m)
考点:相似三角形的应用,解直角三角形的应用
专题:应用题
分析:先根据题意作出几何图,作CF⊥AB于F,延长DC交AB的延长线于E,根据含30度的直角三角形三边的关系得到CF=
BC=1.4,BF=
CF=1.4
,再利用相似得到
=
,计算出EF=
,则AE=AB+BF+EF≈6.758,然后再根据同一时刻的树高与树影的长的比相等得到
=
,然后根据比例性质计算即可.
| 1 |
| 2 |
| 3 |
| 3 |
| CF |
| EF |
| 1.2 |
| 0.8 |
| 14 |
| 15 |
| AD |
| AE |
| 1.2 |
| 0.8 |
解答:解:如图, 作CF⊥AB于F,延长DC交AB的延长线于E,
作CF⊥AB于F,延长DC交AB的延长线于E,
在Rt△BCF中,∵∠CBF=30°,BC=2.8,
∴CF=
BC=1.4,BF=
CF=1.4
,
∵小树的高为1.2m,树影的长为0.8m,
∴
=
,即
=
,
∴EF=
,
∴AE=AB+BF+EF=3.4+1.4
+
≈6.758,
∵
=
,
∴AD=
×6.758≈10.1,
即树AD的高约为10.1m.
 作CF⊥AB于F,延长DC交AB的延长线于E,
作CF⊥AB于F,延长DC交AB的延长线于E,在Rt△BCF中,∵∠CBF=30°,BC=2.8,
∴CF=
| 1 |
| 2 |
| 3 |
| 3 |
∵小树的高为1.2m,树影的长为0.8m,
∴
| CF |
| EF |
| 1.2 |
| 0.8 |
| 1.4 |
| EF |
| 1.2 |
| 0.8 |
∴EF=
| 14 |
| 15 |
∴AE=AB+BF+EF=3.4+1.4
| 3 |
| 14 |
| 15 |
∵
| AD |
| AE |
| 1.2 |
| 0.8 |
∴AD=
| 1.2 |
| 0.8 |
即树AD的高约为10.1m.
点评:本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 在四边形ABCD中,AD∥BC,BD是∠ABC的平分线,且CD⊥BD,AD=4,CD=2.
在四边形ABCD中,AD∥BC,BD是∠ABC的平分线,且CD⊥BD,AD=4,CD=2.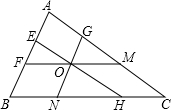 已知O是△ABC内一点,且GN∥AB,FM∥BC,EH∥AC,求证:
已知O是△ABC内一点,且GN∥AB,FM∥BC,EH∥AC,求证: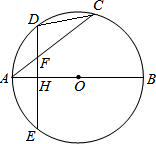 如图,已知AB、AC分别为⊙O的直径和弦,D为
如图,已知AB、AC分别为⊙O的直径和弦,D为
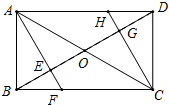 如图,矩形ABCD中,O是两条对角线的交点,AF垂直平分线段OB,垂足为E,CH垂直平分线段OD,垂足为G.求证:
如图,矩形ABCD中,O是两条对角线的交点,AF垂直平分线段OB,垂足为E,CH垂直平分线段OD,垂足为G.求证: 用小立方块搭成的几何体.从正面看和从上面看的形状如图所示,问组成这样的几何体最多需要多少个立方块,最少需要多少个立方块?请画出最少和最多时从左面看到的形状.
用小立方块搭成的几何体.从正面看和从上面看的形状如图所示,问组成这样的几何体最多需要多少个立方块,最少需要多少个立方块?请画出最少和最多时从左面看到的形状.