题目内容
9.计算:(1)4$\sqrt{5}$+$\sqrt{45}$-$\sqrt{20}$;
(2)$\sqrt{32}$-5$\sqrt{\frac{1}{2}}$+6$\sqrt{\frac{1}{8}}$.
分析 (1)根据二次根式的加减运算,先化为最简二次根式,再将被开方数相同的二次根式进行合并;
(2)根据二次根式的加减运算,先化为最简二次根式,再将被开方数相同的二次根式进行合并.
解答 解(1)原式=4$\sqrt{5}$+3$\sqrt{5}$-2$\sqrt{5}$=5$\sqrt{5}$;
(2)原式=4$\sqrt{2}$-$\frac{5}{2}$$\sqrt{2}$+$\frac{3}{2}$$\sqrt{2}$=3$\sqrt{2}$.
点评 本题考查了二次根式的加减法,同类二次根式是指几个二次根式化简成最简二次根式后,被开方数相同的二次根式.二次根式的加减运算,先化为最简二次根式,再将被开方数相同的二次根式进行合并.合并同类二次根式的实质是合并同类二次根式的系数,根指数与被开方数不变.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.点A,B在数轴上所表示的数分别是-8和2,点C是线段AB的中点,则点C在数轴上所表示的数为( )
| A. | -4 | B. | -3 | C. | -2 | D. | -1 |
4.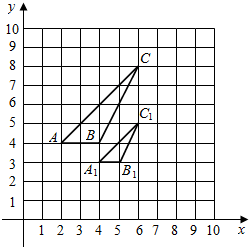 如图,△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心坐标是( )
如图,△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心坐标是( )
 如图,△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心坐标是( )
如图,△ABC与△A1B1C1是位似图形,且顶点都在格点上,则位似中心坐标是( )| A. | (6,2) | B. | (6,1) | C. | (4,2) | D. | (2,6) |
 一条绳子对折后成如图A、B,A,B上一点C,有BC=2AC,将绳子从C点剪断,得到的线段中最长的一段为40cm,请问这条绳子的长度为120cm.
一条绳子对折后成如图A、B,A,B上一点C,有BC=2AC,将绳子从C点剪断,得到的线段中最长的一段为40cm,请问这条绳子的长度为120cm. △ABC中,∠C=90°,∠ABC=45°,D为AC上一点,∠DBC=30°,求AD:AB的值.
△ABC中,∠C=90°,∠ABC=45°,D为AC上一点,∠DBC=30°,求AD:AB的值.