题目内容
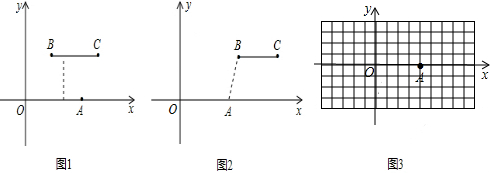
13.(1)如图1,等边三角形ABC与等边△MDE,点M、N、F分别是AB、AC、BC的中点,点D在直线BC上,猜想DF与EN的数量关系.(2)如图2,等腰△ABC与等腰△MDEE,MD=ME,CA=CB,∠DME=∠ACB,点M、N、F分别是AB、AC、BC的中点,点D在直线BC上,DF与EN的关系还成立吗?并说明理由.
(3)如图3,等腰直角△ABC与等腰直角△MDE,∠MDE=∠CAB=90°,点M、N、F分别是AB、AC、BC的中点,点D在直线BC上,试探究$\frac{DF}{EN}$的值.
(4)如图4,任意△ABC与△MDE,∠DME=∠ACB,ME=mDM,BC=mAC,点M、N、F分别是AB、AC、BC的中点,点D在直线BC上,直接写出$\frac{DF}{EN}$的值.
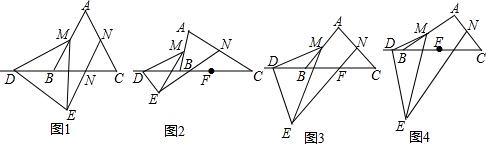
分析 (1)连接MN、MF、NF,如图1,易证△MNF是等边三角形,结合条件△MDE是等边三角形,即可证到△DMF≌△EMN,则有DF=EN;
(2)连接MN、MF、NF,如图2,易证四边形MNCF是菱形,从而可得∠FMN=∠ACB.由∠DME=∠ACB可得∠DME=∠FMN,从而有∠DMF=∠EMN,进而可证到△DMF≌△EMN,则有DF=EN;
(3)连接MN、MF、NF,如图3,易证四边形MNCF是平行四边形,从而可得∠FMN=∠ACB.由∠DME=∠ACB可得∠DME=∠FMN,从而有∠DMF=∠EMN.易证$\frac{ME}{MD}$=$\frac{BC}{AC}$=$\frac{MN}{MF}$,从而可得△DMF∽△EMN,然后运用相似三角形的性质就可解决问题;
(4)连接MN、MF、NF,如图4,仿照(3)的方法,可证到△DMF∽△EMN,然后运用相似三角形的性质就可解决问题.
解答 解:(1)DF=EN.
理由:连接MN、MF、NF,如图1,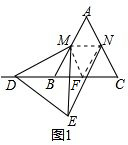
∵点M、N、F分别是AB、AC、BC的中点,
∴MN=$\frac{1}{2}$BC,MF=$\frac{1}{2}$AC,NF=$\frac{1}{2}$AB.
∵△ABC是等边三角形,
∴AB=AC=BC,
∴MN=MF=NF,
∴△MNF是等边三角形,
∴∠NMF=60°.
∵△MDE是等边三角形,
∴MD=ME,∠DME=60°,
∴∠DME=∠FMN,
∴∠DMF=∠EMN.
在△DMF和△EMN中,
$\left\{\begin{array}{l}{MD=ME}\\{∠DMF=∠EMN}\\{MF=MN}\end{array}\right.$,
∴△DMF≌△EMN,
∴DF=EN;
(2)DF=EN仍然成立.
理由:连接MN、MF、NF,如图2,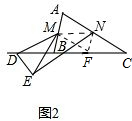
∵点M、N、F分别是AB、AC、BC的中点,
∴MN=$\frac{1}{2}$BC=FC,MF=$\frac{1}{2}$AC=NC,
∵CA=CB,∴MN=MF=FC=NC,
∴四边形MNCF是菱形,
∴∠FMN=∠ACB.
∵∠DME=∠ACB,
∴∠DME=∠FMN,
∴∠DMF=∠EMN.
在△DMF和△EMN中,
$\left\{\begin{array}{l}{MD=ME}\\{∠DMF=∠EMN}\\{MF=MN}\end{array}\right.$,
∴△DMF≌△EMN,
∴DF=EN;
(3)连接MN、MF、NF,如图3,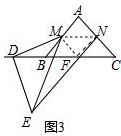
∵点M、N、F分别是AB、AC、BC的中点,
∴MN=$\frac{1}{2}$BC=FC,MF=$\frac{1}{2}$AC=NC,
∴四边形MNCF是平行四边形,
∴∠FMN=∠ACB.
∵△ABC与△MDE都是等腰直角三角形,∠MDE=∠CAB=90°,
∴ME=$\sqrt{2}$MD,BC=$\sqrt{2}$AC,∠DME=45°,∠ACB=45°,
∴$\frac{ME}{MD}$=$\frac{BC}{AC}$,∠DME=∠ACB=∠FMN,
∴$\frac{ME}{MD}$=$\frac{BC}{AC}$=$\frac{MN}{MF}$,∠DMF=∠EMN,
∴△DMF∽△EMN,
∴$\frac{DF}{EN}$=$\frac{DM}{EM}$=$\frac{DM}{\sqrt{2}DM}$=$\frac{\sqrt{2}}{2}$;
(4)$\frac{DF}{EN}$=$\frac{1}{m}$.
提示:连接MN、MF、NF,如图4,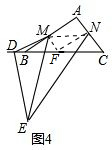
仿照(3)的方法,可证到△DMF∽△EMN,
即可得到$\frac{DF}{EN}$=$\frac{DM}{EM}$=$\frac{DM}{m•DM}$=$\frac{1}{m}$.
点评 本题主要考查了等边三角形的判定与性质、相似三角形的判定与性质、全等三角形的判定与性质、菱形的判定与性质、平行四边形的判定与性质、三角形中位线定理、等腰三角形的性质等知识,综合性强,运用已有经验解决问题是解决本题的关键.

| A. | y=x+3 | B. | y=2x-3 | C. | y=3x-3 | D. | y=4x-4 |
 如图,是一个正方体纸盒的展开图,若在其中三个正方形A、B、C中分别填入适当的数,使得它们折成正方体后相对的面上两个数互为相反数,则填入正方形A、B、C中的三个数依次是( )
如图,是一个正方体纸盒的展开图,若在其中三个正方形A、B、C中分别填入适当的数,使得它们折成正方体后相对的面上两个数互为相反数,则填入正方形A、B、C中的三个数依次是( )| A. | -3、$-\frac{1}{2}$、1 | B. | $-\frac{1}{2}$、-3、1 | C. | 1、-3、$-\frac{1}{2}$ | D. | -3、1、$-\frac{1}{2}$ |
| A. | 1cm | B. | 5cm | C. | 1cm或5cm | D. | 0.5cm或2.5cm |
| A. | y=-2x | B. | y=$\frac{2}{x}$ | C. | y=2x-1 | D. | y=-x2+1 |
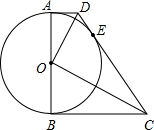 已知:如图,AD、BC与⊙O切于A、B,且AD∥BC,若∠COD=90°
已知:如图,AD、BC与⊙O切于A、B,且AD∥BC,若∠COD=90°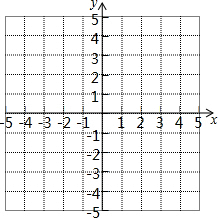 如图,描出A(-3,-2)、B(2,-2)、C(-2,1)、D(3,1)四个点,线段AB、CD有什么关系?顺次连接A、B、C、D四点组成的图形是什么图形?
如图,描出A(-3,-2)、B(2,-2)、C(-2,1)、D(3,1)四个点,线段AB、CD有什么关系?顺次连接A、B、C、D四点组成的图形是什么图形?