题目内容
16.解下列方程组(1)$\left\{\begin{array}{l}{4x-y=1}\\{y=2x+3}\end{array}\right.$
(2)$\left\{\begin{array}{l}{5x+y=2}\\{x-3y=4}\end{array}\right.$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{4x-y=1①}\\{y=2x+3②}\end{array}\right.$,
把②代入①得:4x-2x-3=1,
解得:x=2,
把x=2代入②得:y=7,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=7}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{5x+y=2①}\\{x-3y=4②}\end{array}\right.$,
①×3+②得:16x=10,即x=$\frac{5}{8}$,
把x=$\frac{5}{8}$代入②得:y=-$\frac{9}{8}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{5}{8}}\\{y=-\frac{9}{8}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
6.下面表格列出了函数y=ax2+bx+c(a,b、c是常数,且a≠0),部分x与y对应值,那么方程ax2+bx+c=0的一个根x的取值范围是( )
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y | -0.03 | -0.01 | 0.02 | 0.04 |
| A. | 6<x<6.7 | B. | 6.7<x<6.18 | C. | 6.18<x<6.19 | D. | 6.9<x<9.20 |
 把一个圆球放置在V形架中,如图是它的平面示意图,CA和CB都是圆O的切线,切点分别是A、B,测得∠ACB=60°,且C点到切点B的距离为6cm,则圆球的半径是2$\sqrt{3}$.
把一个圆球放置在V形架中,如图是它的平面示意图,CA和CB都是圆O的切线,切点分别是A、B,测得∠ACB=60°,且C点到切点B的距离为6cm,则圆球的半径是2$\sqrt{3}$.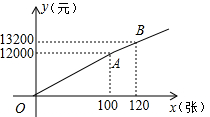 在体育局的策划下,市体育局将组织明星篮球队,为此体育局推出两种购票方案(设购票张数为x,购票总价为y).
在体育局的策划下,市体育局将组织明星篮球队,为此体育局推出两种购票方案(设购票张数为x,购票总价为y).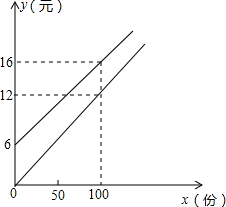 我校实行学案教学,需印刷若干份数学学案.印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示:
我校实行学案教学,需印刷若干份数学学案.印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示: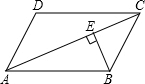 如图所示,在?ABCD中,AC=21cm,BE⊥AC于E,且BE=5cm,AD=7cm,则两条平行线AD与BC间的距离为15cm.
如图所示,在?ABCD中,AC=21cm,BE⊥AC于E,且BE=5cm,AD=7cm,则两条平行线AD与BC间的距离为15cm.