Question

6．如图，已知M是线段AN上的一点，P为NA的中点，Q是AM的中点．求MN：PQ的值．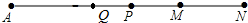

Answer 1

分析 根据线段中点的定义可知：AP=$\frac{1}{2}（AM+MN）$、AQ=$\frac{1}{2}$AM，故QP=AP-AQ=$\frac{1}{2}MN$，然后代入求解即可．

解答 解：∵P是AN的中点，
∴AP=$\frac{1}{2}$AN=$\frac{1}{2}（AM+MN）$．
∵Q是AM的中点，
∴AQ=$\frac{1}{2}$AM．
∴QP=AP-AQ=$\frac{1}{2}（AM+MN）$-$\frac{1}{2}$AM=$\frac{1}{2}MN$．
∴MN：PQ=MN：$\frac{1}{2}$MN=2．

点评 本题主要考查的是两点间的距离，依据线段中点的定义以及线段的和差关系得到PQ=$\frac{1}{2}MN$是解题的关键．