题目内容
5.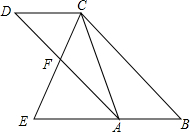 如图,已知:四边形ABCD是平行四边形,点E在边BA的延长线上,CE交AD于点F,∠ECA=∠D
如图,已知:四边形ABCD是平行四边形,点E在边BA的延长线上,CE交AD于点F,∠ECA=∠D(1)求证:△EAC∽△ECB;
(2)若DF=AF,求AC:BC的值.
分析 (1)由四边形ABCD是平行四边形、∠ECA=∠D可得∠ECA=∠B,∠E为公共角可得△EAC∽△ECB;
(2)由CD∥AE、DF=AF可得CD=AE,进而有BE=2AE,根据△EAC∽△ECB得$C{E}^{2}=AE•BE=\frac{1}{2}B{E}^{2}$,即:$\frac{CE}{BE}$=$\frac{\sqrt{2}}{2}$,可得答案.
解答 解:(1)∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵∠ECA=∠D,
∴∠ECA=∠B,
∵∠E=∠E,
∴△EAC∽△ECB;
(2)∵四边形ABCD是平行四边形,
∴CD∥AB,即:CD∥AE
∴$\frac{CD}{AE}=\frac{DF}{AF}$,
∵DF=AF
∴CD=AE,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴AE=AB,
∴BE=2AE,
∵△EAC∽△ECB,
∴$\frac{AE}{CE}=\frac{CE}{BE}=\frac{AC}{BC}$,
∴$C{E}^{2}=AE•BE=\frac{1}{2}B{E}^{2}$,即:$\frac{CE}{BE}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{AC}{BC}=\frac{\sqrt{2}}{2}$.
点评 本题主要考查相似三角形的判定与性质及平行四边形的性质,熟练掌握相似形的对应边成比例和平行四边形的性质是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.若顺次连结四边形ABCD各边中点所得四边形是矩形,则原四边形必定是( )
| A. | 正方形 | B. | 对角线相等的四边形 | ||
| C. | 菱形 | D. | 对角线相互垂直的四边形 |
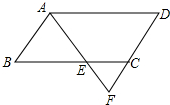 如图,在平行四边形ABCD中,E是BC上一点,且AB=BE,AE的延长线交DC的延长线于点F,若∠F=62°,则∠D=56度.
如图,在平行四边形ABCD中,E是BC上一点,且AB=BE,AE的延长线交DC的延长线于点F,若∠F=62°,则∠D=56度.
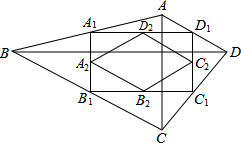 如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,如此进行下去,得到四边形AnBnCnDn.
如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,如此进行下去,得到四边形AnBnCnDn.