题目内容
某商场以每件42元的价钱购进一种服装,根据试销得知:这种服装每天的销售量t(件),与每件的销售价x(元/件)可看成是一次函数关系:t=-3x+204.
(1)写出商场卖这种服装每天的销售利润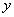 与每件的销售价
与每件的销售价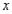 之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);
之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);
(2)通过对所得函数关系式进行配方,指出:商场要想每天获得最大的销售利润,每件的销售价定为多少最为合适;最大销售利润为多少?
当每件的销售价为55元时,可取得最大利润,每天最大销售利润为507元. 【解析】试题分析:(1)商场的利润是由每件商品的利润乘每天的销售的数量所决定.在这个问题中,每件服装的利润为(x-42),而销售的件数是(-3x+204),由销售利润y=(售价-成本)×销售量,那么就能得到一个y与x之间的函数关系,这个函数是二次函数. (2)要求销售的最大利润,就是要求这个二次函数的最大值. ...
练习册系列答案
相关题目
某地新建了一个企业,每月将生产1 960 t污水,为保护环境,该企业计划购置污水处理器,并在如下两个型号中选择:
污水处理器型号 | A型 | B型 |
处理污水能力(t/月) | 240 | 180 |
已知商家售出的2台A型、3台B型污水处理器的总价为44万元,售出的1台A型、4台B型污水处理器的总价为42万元.
(1)求每台A型、B型污水处理器的价格;
(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么至少要支付多少钱?
(1)每台A型污水处理器的价格是10万元,每台B型污水处理器的价格是8万元; (2)买6台A型污水处理器、3台B型污水处理器,费用最少,至少要支付84万元钱. 【解析】试题分析:(1)可设每台A型污水处理器的价格是x万元,每台B型污水处理器的价格是y万元,根据等量关系:①2台A型、3台B型污水处理器的总价为44万元,②1台A型、4台B型污水处理器的总价为42万元,列出方程组求解即可; ...

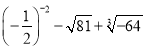 (2)
(2) 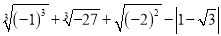
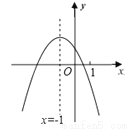

 B.
B. 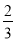 C.
C. 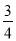 D.
D. 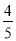
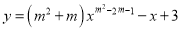 是关于
是关于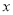 的二次函数,则
的二次函数,则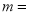 ____________.
____________.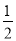 ﹣
﹣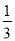 ﹣
﹣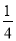 )×(
)×(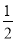 +
+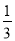 +
+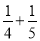 )﹣(1﹣
)﹣(1﹣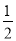 ﹣
﹣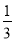 ﹣
﹣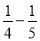 )×(
)×(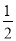 +
+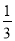 +
+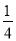 ).
).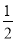 +
+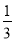 +
+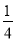 =t,则原式=(1﹣t)(t+
=t,则原式=(1﹣t)(t+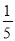 )﹣(1﹣t﹣
)﹣(1﹣t﹣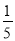 )t=t+
)t=t+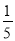 ﹣t2﹣
﹣t2﹣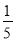 t﹣
t﹣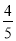 t+t2=
t+t2=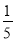 ,
,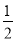 ﹣
﹣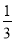 ﹣
﹣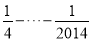 )×(
)×(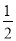 +
+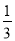 +
+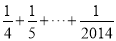 )﹣(1﹣
)﹣(1﹣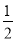 ﹣
﹣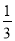 ﹣
﹣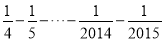 )×(
)×(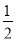 +
+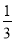 +
+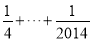 );
);