Question

往直径为680mm的圆柱形油槽内装入一些油以后，截面如图所示，若油面宽AB=600mm，求油的最大深度．

Answer 1

考点：垂径定理的应用,勾股定理

专题：

分析：连接OB，过点O作OC⊥AB于点D，交⊙O于点C，先由垂径定理求出BD的长，再根据勾股定理求出OD的长，进而可得出CD的长．

解答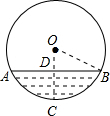：解：过点O作OC⊥AB于点D，交弧AB于点C．
∵OC⊥AB于点D
∴BD=

1

2

AB=

1

2

×600=300mm，
∵⊙O的直径为680mm
∴OB=340mm…（5分）
∵在Rt△ODB中，OD=

OB2-BD2

=

3402-3002

=160（mm），
∴DC=OC-OD=340-160=180（mm）；
答：油的最大深度为180mm．

点评：本题考查的是垂径定理的应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．