题目内容
17.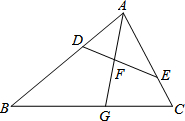 如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且$\frac{AD}{AC}=\frac{DF}{CG}$.
如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且$\frac{AD}{AC}=\frac{DF}{CG}$.(1)求证:△ADF∽△ACG;
(2)若$\frac{AD}{AC}=\frac{1}{2}$,求$\frac{AF}{FG}$的值.
分析 (1)欲证明△ADF∽△ACG,由$\frac{AD}{AC}=\frac{DF}{CG}$可知,只要证明∠ADF=∠C即可.
(2)利用相似三角形的性质得到$\frac{AF}{AG}$=$\frac{1}{2}$,由此即可证明.
解答 (1)证明:∵∠AED=∠B,∠DAE=∠DAE,
∴∠ADF=∠C,
∵$\frac{AD}{AC}$=$\frac{DF}{CG}$,
∴△ADF∽△ACG.
(2)解:∵△ADF∽△ACG,
∴$\frac{AD}{AC}$=$\frac{AF}{AG}$,
又∵$\frac{AD}{AC}$=$\frac{1}{2}$,
∴$\frac{AF}{AG}$=$\frac{1}{2}$,
∴$\frac{AF}{FG}$=1.
点评 本题考查相似三角形的性质和判定、三角形内角和定理等知识,记住相似三角形的判定方法是解决问题的关键,属于基础题中考常考题型.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
8.在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8、7、9、8、8
乙:7、9、6、9、9
则下列说法中错误的是( )
甲:8、7、9、8、8
乙:7、9、6、9、9
则下列说法中错误的是( )
| A. | 甲、乙得分的平均数都是8 | |
| B. | 甲得分的众数是8,乙得分的众数是9 | |
| C. | 甲得分的中位数是9,乙得分的中位数是6 | |
| D. | 甲得分的方差比乙得分的方差小 |
12.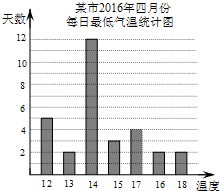 如图是某市2016年四月每日的最低气温(℃)的统计图,则在四月份每日的最低气温这组数据中,中位数和众数分别是( )
如图是某市2016年四月每日的最低气温(℃)的统计图,则在四月份每日的最低气温这组数据中,中位数和众数分别是( )
 如图是某市2016年四月每日的最低气温(℃)的统计图,则在四月份每日的最低气温这组数据中,中位数和众数分别是( )
如图是某市2016年四月每日的最低气温(℃)的统计图,则在四月份每日的最低气温这组数据中,中位数和众数分别是( )| A. | 14℃,14℃ | B. | 15℃,15℃ | C. | 14℃,15℃ | D. | 15℃,14℃ |
2.某班有36人参加义务植树劳动,他们分为植树和挑水两组,要求挑水人数是植树人数的2倍,设有x人挑水,y人植树,则下列方程组中正确的是( )
| A. | $\left\{\begin{array}{l}{2x+y=6}\\{x=2y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+2y=36}\\{y=2x}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=36}\\{x=2y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=36}\\{y=2x}\end{array}\right.$ |

 如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )



 如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,使点A′落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB′=46度.
如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,使点A′落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB′=46度.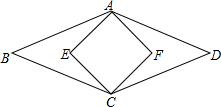 如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为13cm.
如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为13cm. 将等边△CBA绕点C顺时针旋转∠α得到△CB′A′,使得B,C,A′三点在同一直线上,如图所示,则∠α的大小是120°.
将等边△CBA绕点C顺时针旋转∠α得到△CB′A′,使得B,C,A′三点在同一直线上,如图所示,则∠α的大小是120°.