题目内容
6．如图，a、b、c分别是数轴上点A、B、C所对应的实数，试化简：$\sqrt{{b}^{2}}$+|a-c|+$\root{3}{（a+b）^{3}}$．
分析 根据就数轴上点的位置判断出b与a-c的正负，原式利用绝对值的代数意义，平方根、立方根定义计算即可得到结果．
解答 解：根据题意得：b＜a＜0＜c，
∴a-c＜0，
则原式=|b|+c-a+a+b=-b+c-a+a+b=c．
点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
已知△ABC，请在△ABC内确定一个点P，使得点P到AB和BC的距离相等，且满足P到点A和点C的距离相等．（不写作法，保留作图痕迹）．
在△ABC中，AB=AC，AD是△ABC的高，DE⊥AB，DF⊥AC，垂足分别为E、F，（1）途中有哪些全等的三角形？（请一一写出，不需要说明理由）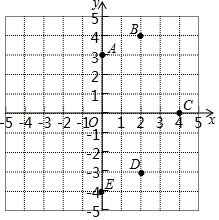
如图，在平面直角坐标系中，已知点A（0，3），B（2，4），C（4，0），D（2，-3），E（0，-4）．
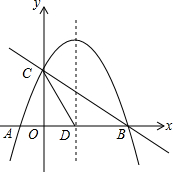如图，抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（-1，0），C（0，2）．
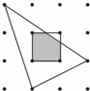如图，平面内有16个格点，每个格点小正方形的边长为1，则图中阴影部分的面积为$\frac{11}{12}$．