题目内容
14.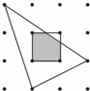 如图,平面内有16个格点,每个格点小正方形的边长为1,则图中阴影部分的面积为$\frac{11}{12}$.
如图,平面内有16个格点,每个格点小正方形的边长为1,则图中阴影部分的面积为$\frac{11}{12}$.
分析 可运用相似三角形的性质求出GF、MN,从而求出OF、OM,进而可求出阴影部分的面积.
解答 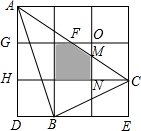 解:如图,
解:如图,
∵GF∥HC,
∴△AGF∽△AHC,
∴$\frac{GF}{HC}$=$\frac{AG}{AH}$=$\frac{1}{2}$,
∴GF=$\frac{1}{2}$HC=$\frac{3}{2}$,
∴OF=OG-GF=2-$\frac{3}{2}$=$\frac{1}{2}$.
同理MN=$\frac{2}{3}$,则有OM=$\frac{1}{3}$.
∴S△OFM=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{3}$=$\frac{1}{12}$,
∴S阴影=1-$\frac{1}{12}$=$\frac{11}{12}$.
故答案为:$\frac{11}{12}$.
点评 本题主要考查了相似三角形的判定与性质、三角形的面积公式,求得△OFM的面积是解决本题的关键.

练习册系列答案
相关题目

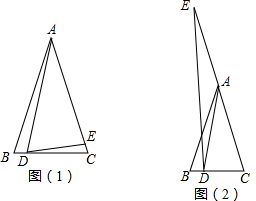
 如图,△ABC是等边三角形,BD是中线,过点D作DE⊥AB于E交BC边延长线于F,AE=1.求BF的长.
如图,△ABC是等边三角形,BD是中线,过点D作DE⊥AB于E交BC边延长线于F,AE=1.求BF的长.