题目内容
4. 如图:在△ABC中,AD⊥BC,垂足是D.
如图:在△ABC中,AD⊥BC,垂足是D.(1)作△ABC的外接圆O(尺规作图);
(2)若AB=8,AC=6,AD=5,求△ABC的外接圆O半径的长.
分析 (1)分别作AB和BC的垂直平分线,它们相交于点O,然后以O点为圆心,OA为半径作圆即可;
(2)作直径AE,连结BE,如图,根据圆周角定理得到∠ABE=90°,∠C=∠E,则可证明Rt△ABE∽Rt△ADC,然后利用相似比计算出AE即可得到△ABC的外接圆O半径的长.
解答 解:(1)如图,⊙O为所作;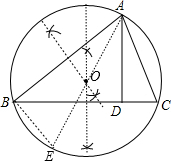
(2)作直径AE,连结BE,如图,
∵AE为直径,
∴∠ABE=90°,
∵AD⊥BC,
∴∠ADC=90°,
∵∠C=∠E,
∴Rt△ABE∽Rt△ADC,
∴$\frac{AE}{AC}$=$\frac{AB}{AD}$,即$\frac{AE}{6}$=$\frac{8}{5}$,
∴AE=$\frac{48}{5}$,
∴OA=$\frac{1}{2}$AE=$\frac{24}{5}$,
即△ABC的外接圆O半径的长为$\frac{24}{5}$.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.解决(2)小题的关键是构建Rt△ABE与△ADC相似.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.为了鼓励市民节约用水,某市制定出一套节水的管理措施,对市民生活用水收费作如下规定:
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)若该户某月用水量为x吨,缴纳水费y元,试列出y关于x的函数式;
(3)若某用户七月份缴纳水费100元,该用户七月份用水量是多少?
| 月用水量(吨) | 单价(元/吨) |
| 不大于10吨部分 | 2.5 |
| 大于10吨不大于20吨部分 | 4 |
| 大于20吨部分 | 5 |
(2)若该户某月用水量为x吨,缴纳水费y元,试列出y关于x的函数式;
(3)若某用户七月份缴纳水费100元,该用户七月份用水量是多少?
19.抛物线y=-2x2-4x-5的顶点坐标是( )
| A. | (1,3) | B. | (-1,3) | C. | (1,-3) | D. | (-1,-3) |
13.若点(-1,m)与(2,n)在直线y=-3x+b上,则m和n的大小关系是( )
| A. | m>n | B. | m<n | C. | m=n | D. | 无法比较 |
 如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连结FG;下列结论:①AE=BD;②AG=BF;③△BCF≌△DCF;④∠BOE=120°.其中正确的是( )
如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连结FG;下列结论:①AE=BD;②AG=BF;③△BCF≌△DCF;④∠BOE=120°.其中正确的是( )