题目内容
20. 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C,若PC=2$\sqrt{5}$,⊙O的半径为( )
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C,若PC=2$\sqrt{5}$,⊙O的半径为( )| A. | $\sqrt{5}$ | B. | $\frac{5}{2}$ | C. | 2$\sqrt{5}$ | D. | 3 |
分析 首先连接OB,利用切线的性质与OP⊥l,易证得∠ACP=∠CBA,即可证得AB=AC,然后设⊙O的半径为x,利用勾股定理,分别表示出AB与AC,即可得方程:(2$\sqrt{5}$)2-(5-r)2=52-r2,继而求得答案.
解答 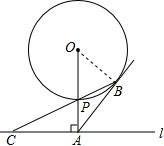 解:连接OB,
解:连接OB,
∵AB为切线,
∴∠OBA=90°,即∠OBP+∠PBA=90°,
∵OA⊥l,
∴∠OAC=90°,
∴∠ACP+∠CPA=90°,
∵OP=OB,
∴∠OPB=∠OBP.
而∠OPB=∠CPA,
∴∠CPA=∠OBP.
∴∠ACP=∠CBA,
∴AB=AC;
设⊙O的半径为r,
在Rt△PAC中,PA=OA-OP=5-r,
∴AC2=PC2-PA2=(2$\sqrt{5}$)2-(5-r)2,
在Rt△ABO中,AB2=OA2-OB2=52-r2,
而AB=AC,
∴(2$\sqrt{5}$)2-(5-r)2=52-r2,解得r=3,
即⊙O的半径为3.
故选D.
点评 此题考查了切线的性质、等腰三角形的判定与性质以及勾股定理.注意掌握方程思想的应用是解此题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
11.下列用数轴表示不等式2-x≤1的解集正确的是( )
| A. | 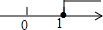 | B. |  | C. |  | D. |  |
12.为了鼓励市民节约用水,某市制定出一套节水的管理措施,对市民生活用水收费作如下规定:
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)若该户某月用水量为x吨,缴纳水费y元,试列出y关于x的函数式;
(3)若某用户七月份缴纳水费100元,该用户七月份用水量是多少?
| 月用水量(吨) | 单价(元/吨) |
| 不大于10吨部分 | 2.5 |
| 大于10吨不大于20吨部分 | 4 |
| 大于20吨部分 | 5 |
(2)若该户某月用水量为x吨,缴纳水费y元,试列出y关于x的函数式;
(3)若某用户七月份缴纳水费100元,该用户七月份用水量是多少?
 已知正比例函数y=$\frac{1}{2}$x的图象与一次函数y=kx-3的图象相交于点(2,a).
已知正比例函数y=$\frac{1}{2}$x的图象与一次函数y=kx-3的图象相交于点(2,a).
