Question

11．如图，AE=AB，AE⊥AB，AC=AF，AC⊥AF，
求证：（1）CE=BF；
（2）∠E0B=90°；
（3）AO平分∠EOF．

Answer 1

分析 （1）根据垂直的定义得到∠BAE=∠CAF=90°，求得∠CAE=∠BAF，推出△CAE≌△BAF，根据全等三角形的性质即可得到结论；
（2）根据全等三角形的性质得到∠AEC=∠ABF推出A，E，B，O四点共圆，根据圆周角定理即可得到结论；
（3）过A作AM⊥BF于F，AN⊥CE于N，得到∠ANE=∠AMB=90°，证得△AEN≌△ABM，根据全等三角形的性质得到AN=AM，由角平分线的判定即可得到结论．

解答 证明：（1）∵AE⊥AB，AC⊥AF，
∴∠BAE=∠CAF=90°，
∴∠CAE=∠BAF，
在△CAE与△BAF中，$\left\{\begin{array}{l}{AE=AB}\\{∠EAC=∠BAF}\\{AC=AF}\end{array}\right.$，
∴△CAE≌△BAF，
∴CE=BF；

（2）∵△CAE≌△BAF，
∴∠AEC=∠ABF，
∴A，E，B，O四点共圆，
∴∠BOE=∠BAE=90°；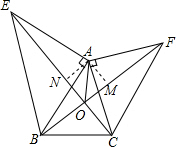

（3）过A作AM⊥BF于F，AN⊥CE于N，
∴∠ANE=∠AMB=90°，
在△ANE与△ABM中，$\left\{\begin{array}{l}{∠AEN=∠ABM}\\{∠ANE=∠AMB}\\{AE=AB}\end{array}\right.$，
∴△AEN≌△ABM，
∴AN=AM，
∴AO平分∠EOF．

点评 本题主要考查全等三角形的判定和性质及等边三角形的、三角形内角和定理的综合应用，熟练掌握全等三角形的判定方法是解题的关键．