题目内容
14. 如图,正方形B的面积是144.
如图,正方形B的面积是144.
分析 根据正方形的面积公式求出AC、AD的长,根据勾股定理求出CD的长,根据正方形的面积公式计算即可.
解答 解: 由正方形的面积公式可知,
由正方形的面积公式可知,
AC=13,AD=5,
由勾股定理得,DC=$\sqrt{A{C}^{2}-A{D}^{2}}$=12,
则CD2=144,
∴正方形B的面积是144,
故答案为:144.
点评 本题考查的是勾股定理的应用,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.

练习册系列答案
相关题目
9.如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )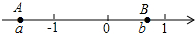
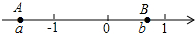
| A. | a+b<0 | B. | a-b>0 | C. | ab>0 | D. | $\frac{a}{b}$>0 |
19.方程3x2-4x-1=0的二次项系数和一次项系数分别为( )
| A. | 3和4 | B. | 3和-4 | C. | 3和-1 | D. | 3和1 |
4.下列四条线段成比例的是( )
| A. | a=2,b=$\sqrt{5}$,c=2$\sqrt{3}$,d=$\sqrt{3}$ | B. | a=$\sqrt{2}$,b=2,c=1,d=$\sqrt{2}$ | ||
| C. | a=4,b=6,c=5,d=10 | D. | a=12,b=8,c=15,d=11 |
 如图,长方形ABCD的长与宽分别是6,4,建立适当的直角坐标系,写出各顶点的坐标.
如图,长方形ABCD的长与宽分别是6,4,建立适当的直角坐标系,写出各顶点的坐标.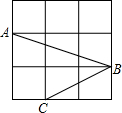 如图,网格中的每个小正方形的边长都是1,A,B,C三点是小正方形的顶点,则∠ABC的度数为45°.
如图,网格中的每个小正方形的边长都是1,A,B,C三点是小正方形的顶点,则∠ABC的度数为45°.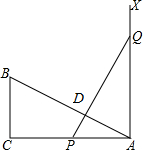 如图,有一个直角三角形ABC,∠C=90°,AB=8,BC=3,P、Q两点分别在边AC和过点A且垂直于AC的射线AX上运动,PQ交AB于点D,且PQ=AB.问当AD=4时,才能使△ABC≌△PQA.
如图,有一个直角三角形ABC,∠C=90°,AB=8,BC=3,P、Q两点分别在边AC和过点A且垂直于AC的射线AX上运动,PQ交AB于点D,且PQ=AB.问当AD=4时,才能使△ABC≌△PQA. 小明看自己设计一个画轴,如图,画轴长为20m,宽为10m,正中央是一个与整个画轴长、宽比例相同的矩形,如果四周边衬所占面积是整个画轴面积的$\frac{16}{25}$,且上、下边衬等宽.左、右边衬等宽.求左、右边衬的宽.
小明看自己设计一个画轴,如图,画轴长为20m,宽为10m,正中央是一个与整个画轴长、宽比例相同的矩形,如果四周边衬所占面积是整个画轴面积的$\frac{16}{25}$,且上、下边衬等宽.左、右边衬等宽.求左、右边衬的宽.