题目内容
5.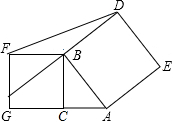 如图所示,在Rt△ABC中,∠ACB=90°,以AB、BC为边向外作正方形ABDE、BCGF,连接DF,且S正方形ABDE=7,S正方形BCGF=3,则△DBF的面积等于$\sqrt{3}$.
如图所示,在Rt△ABC中,∠ACB=90°,以AB、BC为边向外作正方形ABDE、BCGF,连接DF,且S正方形ABDE=7,S正方形BCGF=3,则△DBF的面积等于$\sqrt{3}$.
分析 过点D作DH⊥FB,交FB延长于点H,根据正方形的性质易证△BHD≌△BCA,所以DH=AC,再由已知条件求出AC,BF的长,即可求出△DBF的面积.
解答 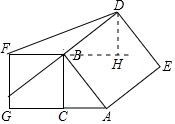 解:过点D作DH⊥FB,
解:过点D作DH⊥FB,
∵以AB、BC为边向外作正方形ABDE、BCGF,
∴∠DBH+∠ABH=90°,∠ABC+∠ABH=90°,BD=AB,
∴∠ABC=∠DBH,
∵∠DHB=∠ACB=90°,
∴在△BHD和△BCA中,
$\left\{\begin{array}{l}{∠DHB=∠ACB=90°}\\{∠DBH=∠ABC}\\{BD=AB}\end{array}\right.$,
∴△BHD≌△BCA(AAS),
∴DH=AC,
∵S正方形ABDE=7,S正方形BCGF=3,
∴AB2=7,BC2=3,
∴AC2=4,BC=BF=$\sqrt{3}$,
∴AC=BH=2,
∴△DBF的面积=$\frac{1}{2}$BF•DH=$\frac{1}{2}$×$\sqrt{3}$×2=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查了勾股定理在直角三角形中的运用,考查了正方形的性质以及面积的计算,本题中正确证明△BHD≌△BCA解题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
16.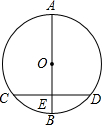 如图,AB是⊙O的直径,弦CD⊥AB于E,CD=16,EB=4,则AE=( )
如图,AB是⊙O的直径,弦CD⊥AB于E,CD=16,EB=4,则AE=( )
 如图,AB是⊙O的直径,弦CD⊥AB于E,CD=16,EB=4,则AE=( )
如图,AB是⊙O的直径,弦CD⊥AB于E,CD=16,EB=4,则AE=( )| A. | 20 | B. | 18 | C. | 16 | D. | 14 |
20.已知△ABC是等边三角形,则cos2A的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
10.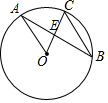 如图,已知⊙O的半径为2,点A、B、C为圆上三点,且OA∥BC,则$\frac{1}{CE}-\frac{1}{BC}$的值是( )
如图,已知⊙O的半径为2,点A、B、C为圆上三点,且OA∥BC,则$\frac{1}{CE}-\frac{1}{BC}$的值是( )
 如图,已知⊙O的半径为2,点A、B、C为圆上三点,且OA∥BC,则$\frac{1}{CE}-\frac{1}{BC}$的值是( )
如图,已知⊙O的半径为2,点A、B、C为圆上三点,且OA∥BC,则$\frac{1}{CE}-\frac{1}{BC}$的值是( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
17.下列运算中正确的是( )
| A. | a3+a3=2a6 | B. | a2•a3=a6 | C. | (a2)3=a5 | D. | a2÷a5=a-3 |
 如图,四边形ABCD中∠A=90°,AB=3cm,AD=4cm,BC=13cm,CD=12cm,求四边形ABCD的面积?
如图,四边形ABCD中∠A=90°,AB=3cm,AD=4cm,BC=13cm,CD=12cm,求四边形ABCD的面积?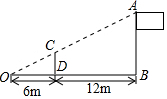 如图,小明用长为2.5m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆的顶端的影子恰好落在地面的同一点O.此时,竹竿与这一点O相距6m、与旗杆相距12m,则旗杆AB的高为7.5m.
如图,小明用长为2.5m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆的顶端的影子恰好落在地面的同一点O.此时,竹竿与这一点O相距6m、与旗杆相距12m,则旗杆AB的高为7.5m.