题目内容
不等式2-m＜x+m的解集为x＞2，则m的值为（ ）
| A、4 | ||
| B、2 | ||
| C、0 | ||
D、
|
考点：解一元一次不等式
专题：
分析：先解出x的取值范围，再根据x＞2，列出关于m的方程，解答即可．
解答：解：移项，得-x＜m+m-2，
合并同类项，得-x＜2m-2，
系数化为1，得x＞-2m+2，
∵不等式2-m＜x+m的解集为x＞2，
∴-2m+2=2，
解得m=0，
故选C．
合并同类项，得-x＜2m-2，
系数化为1，得x＞-2m+2，
∵不等式2-m＜x+m的解集为x＞2，
∴-2m+2=2，
解得m=0，
故选C．
点评：本题考查了解一元一次不等式，知道不等式解集的唯一性是解题的关键．
练习册系列答案
相关题目
为了解赵化学区2013-2014学年度上学期900名七年级学生的期末数学成绩情况，从中抽取的部分学生的数学成绩作为样本，并制成了频数分布直方图（如图所示），则此次抽查的样本容量为
把一个长方形的纸按如图所示的方式折叠后，C，D两点落在C′，D′点处，若∠OGC′=125°，则∠AOD′的度数是（ ）| A、50° | B、60° |
| C、70° | D、80° |
不等式组
的解集是（ ）
|
| A、x＞2 | B、x＞1 |
| C、1＜x＜2 | D、无解 |
小亮在解不等式组
时，解法步骤如下：
解不等式①，得x＞3，…第一步；
解不等式②，得x＞-8，…第二步；
所有原不等式组组的解集为-8＜x＜3…第三步．
对于以上解答，你认为下列判断正确的是（ ）
|
解不等式①，得x＞3，…第一步；
解不等式②，得x＞-8，…第二步；
所有原不等式组组的解集为-8＜x＜3…第三步．
对于以上解答，你认为下列判断正确的是（ ）
| A、解答有误，错在第一步 |
| B、解答有误，错在第二步 |
| C、解答有误，错在第三步 |
| D、原解答正确无误 |
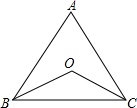如图所示，在△ABC中，AB=AC，∠ABC和∠ACB的平分线相交于点O．试判断△OBC的形状，并说明理由．