题目内容
17.把几个数用大括号围起来,中间用逗号断开,如:{1,2,-3}、{-2,7,$\frac{3}{4}$,19},我们称之为集合,其中的每个数称为该集合的元素.如果一个所有元素均为有理数的集合满足:当有理数a是集合的元素时,2015-a也必是这个集合的元素,这样的集合我们称为好的集合.例如集合{2015,0}就是一个好的集合.(1)集合{2015}不是好的集合,集合{-1,2016}是好的集合(两空均填“是”或“不是”);
(2)若一个好的集合中最大的一个元素为4001,则该集合是否存在最小的元素?如果存在,请直接写出答案,否则说明理由;
(3)若一个好的集合所有元素之和为整数M,且22161<M<22170,则该集合共有几个元素?说明你的理由.
分析 (1)根据有理数a是集合的元素时,2015-a也必是这个集合的元素,这样的集合我们称为好的集合,从而可以可解答本题;
(2)根据2015-a,如果a的值越大,则2015-a的值越小,从而可以解答本题;
(3)根据题意可知好的集合都是成对出现的,并且这对对应元素的和为2015,然后通过估算即可解答本题.
解答 解;(1)根据题意可得,2015-2015=0,而集合{2015}中没有元素0,故{2015}不是好的集合;
∵2015-(-1)=2016,2015-2016=-1,
∴集合{-1,2016}是好的集合.
故答案为:不是,是.
(2)一个好的集合中最大的一个元素为4001,则该集合存在最小的元素,该集合最小的元素是-1986.
∵2015-a中a的值越大,则2015-a的值越小,
∴一个好的集合中最大的一个元素为4001,则最小的元素为:2015-4001=-1986.
(3)该集合共有22个元素.
理由:∵在好的集合中,如果一个元素为a,则另一个元素为2015-a,
∴好的集合中的元素一定是偶数个.
∵好的集合中的每一对对应元素的和为:a+2015-a=2015,2015×11=22165,2015×10=20150,2015×12=24180,
又∵一个好的集合所有元素之和为整数M,且22161<M<22170,
∴这个好的集合中的元素个数为:11×2=22个.
点评 本题考查探究性问题,关键是明确什么是好的集合,集合中的各个数都是元素,明确好的集合中的元素个数都是偶数个,在此还要应用到估算的知识.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.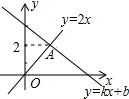 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象相交于点A,则不等式
如图,一次函数y=kx+b的图象与正比例函数y=2x的图象相交于点A,则不等式
0<2x<kx+b的解集是( )
 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象相交于点A,则不等式
如图,一次函数y=kx+b的图象与正比例函数y=2x的图象相交于点A,则不等式0<2x<kx+b的解集是( )
| A. | x<1 | B. | x<0或x>1 | C. | 0<x<1 | D. | x>1 |
12.雾霾天气影响着我国北方中东部地区,给人们的健康带来严重的危害.为了让人们对雾霾有所了解.摄影师张超通过显微镜,将空气中细小的霾颗粒放大1000倍,发现这些霾颗粒平均直径为10微米〜20微米,其中20微米(1米=1000000微米)用科学记数法可表示为( )
| A. | 2×105米 | B. | 0.2×10-4米 | C. | 2×10-5米 | D. | 2×10-4米 |
7.下列各组数中,不是互为相反意义的量的是( )
| A. | 收入200元与支出200元 | B. | 上升7米和下降8米 | ||
| C. | 超过0.05mm与不足0.05mm | D. | 增多2件与减少2升 |
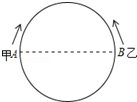 如图所示,甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(cm)与时间t(s)满足关系:l=$\frac{1}{2}{t^2}+\frac{3}{2}$t(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
如图所示,甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(cm)与时间t(s)满足关系:l=$\frac{1}{2}{t^2}+\frac{3}{2}$t(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.