题目内容
9.(1)如图(1),将△ABC纸片沿着DE对折,使点A落在四边形BCDE内点A′的位置,探索∠A,∠1,∠2之间的数量关系,并说明理由.(2)如图(2),继续这样的操作,把△ABC纸片的三个角按(1)的方式折叠,三个顶点都在形内,那么∠1+∠2+∠3+∠4+∠5+∠6的度数是360°.
(3)如果把n边形纸片也做类似的操作,n个顶点都在形内,那么∠1+∠2+∠3+…+∠2n的度数是360°(n-2) (用含有n的代数式表示).
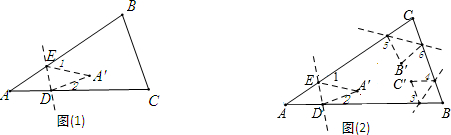
分析 (1)运用折叠原理及四边形的内角和定理即可解决问题;
(2)由折叠可知∠1+∠2+∠3+∠4+∠5+∠6=∠B+∠B'+∠C+∠C'+∠A+∠A',又知∠B=∠B',∠C=∠C',∠A=∠A',故能求出∠1+∠2+∠3+∠4+∠5+∠6的度数和;
(3)利用(1)(2)的计算方法:类比得出答案即可.
解答 解:(1)连接AA′,
∵∠1=∠BAA′+∠AA′E,∠2=∠CAA′+∠AA′D,
∴∠1+∠2=∠BAA′+∠AA′E+∠CAA′+∠AA′D=∠BAC+∠DA′E,
又∵∠BAC=∠DA′E,
∴∠1+∠2=2∠BAC;
(2)∠1+∠2+∠3+∠4+∠5+∠6=∠B+∠B'+∠C+∠C'+∠A+∠A',
∵∠B=∠B',∠C=∠C',∠A=∠A',
∴∠1+∠2+∠3+∠4+∠5+∠6=2(∠B+∠C+∠A)=360°;
(3)∠1+∠2+∠3+…+∠2n
=2(∠B+∠C+∠A)(n-2)
=360°(n-2).
点评 本题考查图形的折叠与拼接,同时考查了三角形、四边形等几何基本知识,掌握折叠的性质是解决问题的关键.

练习册系列答案
相关题目
18.下列说法正确的是( )
| A. | 两点之间,线段最短 | |
| B. | 射线就是直线 | |
| C. | 两条射线组成的图形叫做角 | |
| D. | 小于平角的角可分为锐角和钝角两类 |
 如图是万达广场一楼与二楼之间的手扶电梯示意图.其中AB、CD分别表示一楼、二楼地面的水平线,小马虎从点A到点C共走了12m,电梯上升的高度h为6m,经小马虎测量AB=2,求BE的长度.
如图是万达广场一楼与二楼之间的手扶电梯示意图.其中AB、CD分别表示一楼、二楼地面的水平线,小马虎从点A到点C共走了12m,电梯上升的高度h为6m,经小马虎测量AB=2,求BE的长度.