题目内容
9.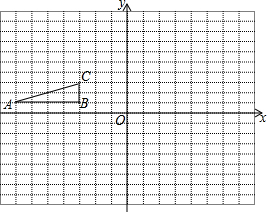 如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-7,1),点B的坐标为(-3,1),点C的坐标为(-3,3).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-7,1),点B的坐标为(-3,1),点C的坐标为(-3,3).(1)若P(m,n)为Rt△ABC内一点,平移Rt△ABC得到Rt△A1B1C1,使点P(m,n)移到点P1(m+6,n)处,试在图上画出Rt△A1B1C1,并直接写出点A1的坐标为(-1,1);
(2)将原来的Rt△ABC绕点B顺时针旋转90°得到Rt△A2B2C2,试在图上画出Rt△A2B2C2,并直接写出点A到A2运动路线的长度为2π;
(3)将Rt△A1B1C1绕点Q旋转90°可以和Rt△A2B2C2完全重合,请直接写出点Q的坐标为(0,4).
分析 (1)由点P(m,n)移到点P1(m+6,n)处,得到三角形ABC向右移动6个单位得到Rt△A1B1C1,画出相应的图形,找出A1坐标即可;
(2)以B为旋转中心,将原来的Rt△ABC绕点B顺时针旋转90°得到Rt△A2B2C2,画出图形,点A到A2运动路线的长度为弧AA2的长,利用弧长公式求出即可;.
(3)在图形中找出P(0,4),可将Rt△A1B1C1绕点P旋转90°可以和Rt△A2B2C2完全重合
解答  解:(1)根据题意得:Rt△ABC向右平移6个单位得到Rt△A1B1C1,作出图形,如图所示,点A1的坐标为(-1,1);
解:(1)根据题意得:Rt△ABC向右平移6个单位得到Rt△A1B1C1,作出图形,如图所示,点A1的坐标为(-1,1);
(2)如图所示,Rt△A2B2C2为所求的三角形,
∵∠ABA2=90°,AB=4,
∴点A到A2运动路线的长度为弧AA2的长l=$\frac{90×π×4}{180}=2π$;
(3)如图所示,当P(0,4)时,Rt△A1B1C1绕点P旋转90°可以和Rt△A2B2C2完全重合.
故答案为:(1)(-1,1);(2)2π;(3)(0,4).
点评 此题考查了作图-旋转变换、平移变换,作出正确的图形是解本题的关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
16.若4个数6,x,8,10的中位数为7,则x的取值范围是( )
| A. | x=6 | B. | x=7 | C. | x≤6 | D. | x≥8 |
17.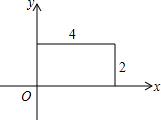 如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )
如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )
 如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )
如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )| A. | (4,0) | B. | (2,4) | C. | (0,2) | D. | (4,2) |
19.下列说法中,正确的是( )
| A. | 内错角相等 | B. | 同旁内角互补 | ||
| C. | 相等的角是对顶角 | D. | 同位角相等两直线平行 |
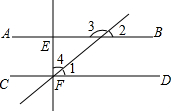 如图,AB∥CD,∠3:∠2=3:2,EF⊥CD,求∠4的度数.
如图,AB∥CD,∠3:∠2=3:2,EF⊥CD,求∠4的度数. 如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,
如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,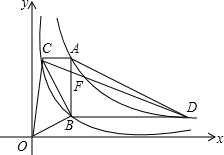 【问题情境】反比例函数y=$\frac{2}{x}$和y=$\frac{8}{x}$在平面直角坐标系xOy第一象限的图象如图所示,点A在y=$\frac{8}{x}$的图象上,AB∥y轴,与y=$\frac{2}{x}$的图象交于点B,AC、BD与x轴平行,分别与y=$\frac{2}{x}$、y=$\frac{8}{x}$的图象交于点C、D.点A、B、C、D的纵坐标分别记为yA、yB、yC、yD,记点A的横坐标为m(m>0).
【问题情境】反比例函数y=$\frac{2}{x}$和y=$\frac{8}{x}$在平面直角坐标系xOy第一象限的图象如图所示,点A在y=$\frac{8}{x}$的图象上,AB∥y轴,与y=$\frac{2}{x}$的图象交于点B,AC、BD与x轴平行,分别与y=$\frac{2}{x}$、y=$\frac{8}{x}$的图象交于点C、D.点A、B、C、D的纵坐标分别记为yA、yB、yC、yD,记点A的横坐标为m(m>0).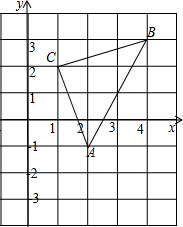 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).