题目内容
12. 利用所示图来证明勾股定理.
利用所示图来证明勾股定理.证明:
分析 用面积分割法法证明勾股定理:梯形的面积=3个三角形面积的和,依此即可证明.
解答 证明:梯形的面积为 $\frac{1}{2}$(a+b)(a+b)=$\frac{1}{2}$(a+b)2;
另一方面,梯形可分成三个直角三角形,其面积又可以表示成 $\frac{1}{2}$ab+$\frac{1}{2}$ab+$\frac{1}{2}$c2.
所以,$\frac{1}{2}$(a+b)2=$\frac{1}{2}$ab+$\frac{1}{2}$ab+$\frac{1}{2}$c2.
即a2+b2=c2.
点评 本题考查了勾股定理的证明,难点在于利用梯形的面积列出方程.

练习册系列答案
相关题目
7.已知点A(2,-3),线段AB与坐标轴平行,则点B的坐标可能是( )
| A. | (-1,-2) | B. | (3,-2) | C. | (1,2) | D. | (-2,-3) |
17.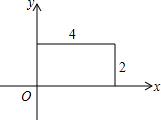 如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )
如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )
 如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )
如图,一个矩形的两边长分别是4和2,建立直角坐标系,则下列不在矩形上的点为( )| A. | (4,0) | B. | (2,4) | C. | (0,2) | D. | (4,2) |
 某班主任把本班学生上学方式的调查结果绘制成如图所示的不完整的统计图,已知骑自行车上学的学生有26人,则采用其他方式上学的学生人数为4 人.
某班主任把本班学生上学方式的调查结果绘制成如图所示的不完整的统计图,已知骑自行车上学的学生有26人,则采用其他方式上学的学生人数为4 人.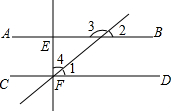 如图,AB∥CD,∠3:∠2=3:2,EF⊥CD,求∠4的度数.
如图,AB∥CD,∠3:∠2=3:2,EF⊥CD,求∠4的度数. 如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,
如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,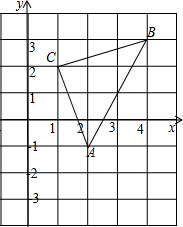 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).