题目内容
16.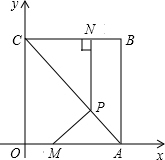 如图,平面直角坐标系中,四边形OABC为矩形,其中点A,C分别在x轴和y轴上,点B的坐标为(3,4),点M,N分别是OA,BC边上的动点,且OM=BN,过点N作NP⊥BC于点P,连接MP,设OM=m(0<m<3)
如图,平面直角坐标系中,四边形OABC为矩形,其中点A,C分别在x轴和y轴上,点B的坐标为(3,4),点M,N分别是OA,BC边上的动点,且OM=BN,过点N作NP⊥BC于点P,连接MP,设OM=m(0<m<3)(1)求点P的坐标(用含m的代数式表示);
(2)若△MPA是等腰三角形,求m的值.
分析 (1)根据PG和OG的长度即可求得P的坐标;
(2)△MPA为等腰三角形,则PM=PA或PM=MA或PA=AM即可,分别求m的值即可.
解答 解:(1)延长NP交OA于G,如图所示:
∵NP⊥BC,四边形OABC为矩形,
∴PN⊥OA,四边形ABNG为矩形,
∵OM=BN,OM=m,
∴BN=m, CN=OG=3-m,
CN=OG=3-m,
∵∠ACB=∠PCN,∠ABC=∠PNC=90°,
∴△CPN∽△CAB,
∴$\frac{PN}{AB}$=$\frac{CN}{CB}$,
∵四边形OABC为矩形,点B的坐标为(3,4),
∴AB=4,BC=3,
∴PN=$\frac{4}{3}$(3-m),
则PG=NG-NP=4-$\frac{4}{3}$(3-m)=$\frac{4}{3}$m,
∴P点的坐标为 (3-m,$\frac{4}{3}$m);
(2)△MPA为等腰三角形有以下三种情况:
①当AP=PM时,AG=MG,
∵四边形ABNG为矩形,
∴AG=BN=m,
MG=OA-OM-AG=3-m-m=3-2m,
∴3-2m=m,
解得:m=1;
②当AM=AP时,则AM=3-m,AP=$\sqrt{A{G}^{2}+P{G}^{2}}$=$\sqrt{{m}^{2}+(\frac{4}{3}m)^{2}}$=$\frac{5}{3}$m,
∴3-m=$\frac{5}{3}$m,
解得:x=$\frac{9}{8}$;
③当PM=AM,则AM=3-m,PM=$\sqrt{M{G}^{2}+P{G}^{2}}$=$\sqrt{(3-2m)^{2}+(\frac{4}{3}m)^{2}}$,
∴3-m=$\sqrt{(3-2m)^{2}+(\frac{4}{3}m)^{2}}$,
解得:m=$\frac{54}{43}$;
综上所述:m=1或$\frac{9}{8}$或$\frac{54}{43}$时,△MPA为等腰三角形.
点评 本题考查了矩形的性质、等腰三角形的判定、坐标与图形性质、勾股定理、相似三角形的判定与性质;本题综合性强,难度较大,特别是(2)中,需要进行分类讨论,才能得出结果.

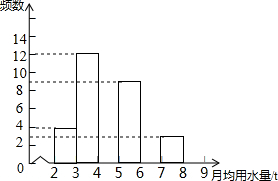 旬阳县在实施定额用水管理前,对城镇6000户居民生活用月均用水情况(单位:t)进行了简单随机抽样调查,并将调查结果绘制成频数分布表和频数分布直方图.
旬阳县在实施定额用水管理前,对城镇6000户居民生活用月均用水情况(单位:t)进行了简单随机抽样调查,并将调查结果绘制成频数分布表和频数分布直方图.(1)补全频数分布表和频数分布直方图;
(2)用扇形统计图表示各用水段居民户占总居民户的百分比;
(3)为了鼓励居民节约用水,县自来水公司要确定一个用水量的标准,超出这个标准的部分按照2倍的价格收费,且要保证60%以上的家庭水费支出不受影响,你觉得家庭月均用水量应定为多少?为什么?在额定标准下,估计有多少户居民家庭水费支出较前有所增加?
| 月均用水量 | 频数 | 百分比 |
| 2≤x<3 | 4 | 8% |
| 3≤x<4 | 12 | 24% |
| 4≤x<5 | 14 | 28% |
| 5≤x<6 | 9 | 18% |
| 6≤x<7 | 6 | 12% |
| 7≤x<8 | 3 | 6% |
| 8≤x<9 | 2 | 4% |
| 合计 | 50 | 100% |
 如图,点0是△ABC的∠ABC、∠ACB的平分线的交点,
如图,点0是△ABC的∠ABC、∠ACB的平分线的交点, 如图,化简:2+|a-2|+|b-2|.
如图,化简:2+|a-2|+|b-2|. 如图,在四边形ABCD中,∠A=∠C,BE平分∠ABC,DF平分∠ADC,求证:BE∥DF.
如图,在四边形ABCD中,∠A=∠C,BE平分∠ABC,DF平分∠ADC,求证:BE∥DF.