Question

18．如图所示，在△ABD中，E是内心，∠BAD的平分线交过△ABD三个顶点的圆（三角形的外接圆）于点C，求证：EC=BC．

Answer 1

分析 首先连接BE，由在△ABD中，E是内心，易得∠BAC=∠CAD，∠ABE=∠DBE，继而可得∠CBE=∠CEB，则可证得结论．

解答 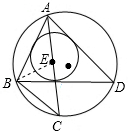证明：连接BE，
∵在△ABD中，E是内心，
∴∠BAC=∠CAD，∠ABE=∠DBE，
∵∠CBD=∠CAD，
∴∠CBD=∠CAB，
∵∠CBE=∠CBD+∠DBE，∠CEB=∠CAB+∠ABE，
∴∠CBE=∠CEB，
∴EC=BC．

点评 此题考查了三角形内切圆的性质与三角形外接圆的性质．注意准确作出辅助线是解此题的关键．