题目内容
18.甲、乙两地相距s千米,原计划用a小时从甲地到达乙地.为了执行新的任务,现需提前1小时到达,则原计划的速度为$\frac{s}{a}$千米/时,实际行驶的速度为$\frac{s}{a-1}$千米/时,若s=100,a=4,则原计划的速度和实际行驶的速度分别为25千米/时和33$\frac{1}{3}$千米/时.分析 利用路程÷时间=速度,分别得出原计划的速度和实际行驶的速度即可;进一步代入数值求得答案即可.
解答 解:原计划的速度为s÷a=$\frac{s}{a}$千米/时,
实际行驶的速度为s÷(a-1)=$\frac{s}{a-1}$千米/时,
当s=100,a=4时,
原计划的速度为$\frac{s}{a}$=$\frac{100}{4}$=25千米/时,
实际行驶的速度为$\frac{s}{a-1}$=$\frac{100}{4-1}$=33$\frac{1}{3}$千米/时.
故答案为:$\frac{s}{a}$千米/时,$\frac{s}{a-1}$千米/时;25千米/时,33$\frac{1}{3}$千米/时.
点评 此题考查列代数式,掌握路程、时间、速度三者之间的关系是解决问题的关键.

练习册系列答案
相关题目
13.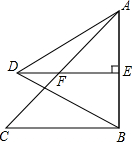 如图,△ABC是等腰直角三角形,∠ABC=90°,AB=10,以AB为边向左边作一个等边△ABD,过点D作DE⊥AB于点E,交AC于点F.
如图,△ABC是等腰直角三角形,∠ABC=90°,AB=10,以AB为边向左边作一个等边△ABD,过点D作DE⊥AB于点E,交AC于点F.
(1)求证:△AEF是等腰直角三角形;
(2)求DF的长.
 如图,△ABC是等腰直角三角形,∠ABC=90°,AB=10,以AB为边向左边作一个等边△ABD,过点D作DE⊥AB于点E,交AC于点F.
如图,△ABC是等腰直角三角形,∠ABC=90°,AB=10,以AB为边向左边作一个等边△ABD,过点D作DE⊥AB于点E,交AC于点F.(1)求证:△AEF是等腰直角三角形;
(2)求DF的长.
3.下列说法正确的是( )
| A. | 任何有理数都有倒数 | |
| B. | 一个数的倒数-定小于这个数 | |
| C. | 倒数等于它本身的数有±1和0 | |
| D. | 一个有理数的倒数的符号与它本身的符号相同 |
10.判定△ABC∽△A′B′C′,已知∠C′=∠C=90°,则应有哪个条件( )
| A. | ∠B=∠B′ | B. | $\frac{A′B′}{AB}$=$\frac{A′C′}{AC}$ | C. | $\frac{B′C′}{BC}$=$\frac{A′C′}{AC}$ | D. | 以上说法都对 |
8.已知半径为5的⊙O中,弦AB=5$\sqrt{2}$,弦AC=5,则∠BOC的度数是( )
| A. | 15° | B. | 210° | C. | 210°或30° | D. | 60°或90° |
 某学校为了改善教职工居住条件,准备在教学楼的正南方建筑一栋住宅楼.要求教学楼与住宅楼等高.均为15.6m.已知该地区冬至正午时分太阳高度最低,太阳光线与水平线的夹角为30°,教学楼与住宅楼相距19.2m,如图所示,
某学校为了改善教职工居住条件,准备在教学楼的正南方建筑一栋住宅楼.要求教学楼与住宅楼等高.均为15.6m.已知该地区冬至正午时分太阳高度最低,太阳光线与水平线的夹角为30°,教学楼与住宅楼相距19.2m,如图所示,