题目内容
13.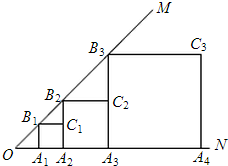 如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,周长记作L1;再作第二个正方形A2B2C2A3,周长记作L2;继续作第三个正方形A3B3C3A4,周长记作L3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第n个正方形的周长Ln=2n+1.
如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,周长记作L1;再作第二个正方形A2B2C2A3,周长记作L2;继续作第三个正方形A3B3C3A4,周长记作L3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第n个正方形的周长Ln=2n+1.
分析 根据题意确定出第一个,第二个,第三个正方形的边长,进而求出周长,以此类推得到一般性规律,即可确定出第n个正方形的周长.
解答 解:根据题意得:第一个正方形的边长为A1A2=A1B1=0A1=1,周长L1=4=22;
第二个正方形的边长为A2B2=OA2=2,周长L2=8=23;
第三个正方形的边长为A3B3=OA3=4,周长L3=16=24;
以此类推,第n个正方形的周长Ln=2n+1.
故答案为:2n+1.
点评 此题考查了正方形的性质,等腰直角三角形的性质,熟练掌握正方形的性质是解本题的关键.

练习册系列答案
相关题目
3.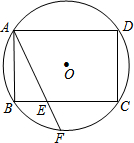 如图,矩形ABCD为⊙O的内接四边形,AB=2,BC=3,点E为BC上一点,且BE=1,延长AE交⊙O于点F,则线段AF的长为( )
如图,矩形ABCD为⊙O的内接四边形,AB=2,BC=3,点E为BC上一点,且BE=1,延长AE交⊙O于点F,则线段AF的长为( )
 如图,矩形ABCD为⊙O的内接四边形,AB=2,BC=3,点E为BC上一点,且BE=1,延长AE交⊙O于点F,则线段AF的长为( )
如图,矩形ABCD为⊙O的内接四边形,AB=2,BC=3,点E为BC上一点,且BE=1,延长AE交⊙O于点F,则线段AF的长为( )| A. | $\frac{7}{5}$$\sqrt{5}$ | B. | 5 | C. | $\sqrt{5}$+1 | D. | $\frac{3}{2}$$\sqrt{5}$ |
2.下列计算正确的是( )
| A. | -3-(-2)=-1 | B. | -3-2=-1 | C. | -3÷2×2=-$\frac{3}{4}$ | D. | -(-1)2=1 |
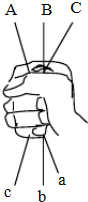 如图,晓明手里拿着三根绳子,小丽负责将两个绳头(大写字母)接好,小菊负责把两个绳尾(小写字母)接好,然后晓明把手松开,他俩正好结成一个环形的概率是多少?(请用树状图或图表分析)
如图,晓明手里拿着三根绳子,小丽负责将两个绳头(大写字母)接好,小菊负责把两个绳尾(小写字母)接好,然后晓明把手松开,他俩正好结成一个环形的概率是多少?(请用树状图或图表分析) 如图,反比例函数y=$\frac{k}{x}$在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4).
如图,反比例函数y=$\frac{k}{x}$在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4).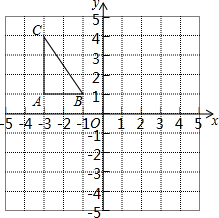 如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.
如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示. 在2014年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数、方差依次是18,18,1.
在2014年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数、方差依次是18,18,1.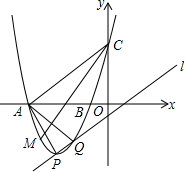 已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1.
已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1.