题目内容
1.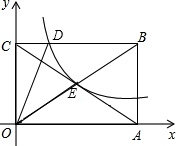 如图,反比例函数y=$\frac{k}{x}$在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4).
如图,反比例函数y=$\frac{k}{x}$在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4).(1)求E点的坐标及k的值;
(2)求△OCD的面积.
分析 (1)由E是矩形OABC对角线的交点,得到OE=EB,由于点B的坐标为(6,4),于是得到E点的坐标是(3,2),即可得到结论;
(2)设点D的坐标为(x,y),即S△OCD=$\frac{1}{2}$xy=$\frac{1}{2}$k=3.
解答 解:(1)∵E是矩形OABC对角线的交点,
∴OE=EB,
∵点B的坐标为(6,4),
∴E点的坐标是(3,2),
把x=3,y=2代入y=$\frac{k}{x}$得k=6;
(2)设点D的坐标为(x,y),则S△OCD=$\frac{1}{2}$OC×OD,
即S△OCD=$\frac{1}{2}$xy=$\frac{1}{2}$k,
由(1)知k=6,
∴S△OCD=$\frac{1}{2}$k=3.
点评 本题考查了待定系数法求函数的解析式,反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|,

练习册系列答案
相关题目
16.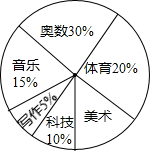 实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
(1)七年级共有学生360人;
(2)在表格中的空格处填上相应的数字;
(3)表格中所提供的六个数据的中位数是63;
(4)众数是72.
 实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.| 学习小组 | 体育 | 美术 | 科技 | 音乐 | 写作 | 奥数 |
| 人数 | 72 | 36 | 54 | 18 |
(2)在表格中的空格处填上相应的数字;
(3)表格中所提供的六个数据的中位数是63;
(4)众数是72.
 如图,已知△OAB的三个顶点的坐标分别为O(0,0)、A(-3,1)、B(0,5),三角形内有任意一点P坐标为(a,b)
如图,已知△OAB的三个顶点的坐标分别为O(0,0)、A(-3,1)、B(0,5),三角形内有任意一点P坐标为(a,b) 如图,在平面直角坐标中,过点A(4,0)的抛物线y=-x2+bx与直线y=-x+b交于另一点B.过抛物线y=-x2+bx的顶点E作EF⊥x轴于F点,点M(t,d)为抛物线y=-x2+bx在x轴上方的动点.
如图,在平面直角坐标中,过点A(4,0)的抛物线y=-x2+bx与直线y=-x+b交于另一点B.过抛物线y=-x2+bx的顶点E作EF⊥x轴于F点,点M(t,d)为抛物线y=-x2+bx在x轴上方的动点. 如图,已知:在△ABC中,D是边AB上的一点,且BC=BD,求证:∠ACB>∠A.
如图,已知:在△ABC中,D是边AB上的一点,且BC=BD,求证:∠ACB>∠A.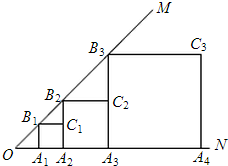 如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,周长记作L1;再作第二个正方形A2B2C2A3,周长记作L2;继续作第三个正方形A3B3C3A4,周长记作L3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第n个正方形的周长Ln=2n+1.
如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,周长记作L1;再作第二个正方形A2B2C2A3,周长记作L2;继续作第三个正方形A3B3C3A4,周长记作L3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第n个正方形的周长Ln=2n+1.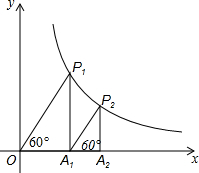 如图,P1是反比例函数y=$\frac{k}{x}$(k>0)在第一象限图象上一点,点A1的坐标为(1,0).
如图,P1是反比例函数y=$\frac{k}{x}$(k>0)在第一象限图象上一点,点A1的坐标为(1,0).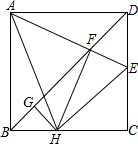 如图,在正方形ABCD中,AB=4,点E为CD上一动点,AE交BD于点F,过点F作FH⊥AE,交BC于H,过H作GH⊥BD于点G,下列结论:①AF=FH,②∠HAE=45°,③BD=$\frac{3}{2}$FG,④△CEH的周长为定值.其中正确的是①②④(写正确结论的序号).
如图,在正方形ABCD中,AB=4,点E为CD上一动点,AE交BD于点F,过点F作FH⊥AE,交BC于H,过H作GH⊥BD于点G,下列结论:①AF=FH,②∠HAE=45°,③BD=$\frac{3}{2}$FG,④△CEH的周长为定值.其中正确的是①②④(写正确结论的序号).