题目内容
4.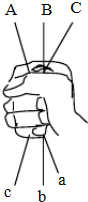 如图,晓明手里拿着三根绳子,小丽负责将两个绳头(大写字母)接好,小菊负责把两个绳尾(小写字母)接好,然后晓明把手松开,他俩正好结成一个环形的概率是多少?(请用树状图或图表分析)
如图,晓明手里拿着三根绳子,小丽负责将两个绳头(大写字母)接好,小菊负责把两个绳尾(小写字母)接好,然后晓明把手松开,他俩正好结成一个环形的概率是多少?(请用树状图或图表分析)
分析 首先根据题意列出表格,然后由表格即可求得所有等可能的结果与这三根绳子能连结成一根长绳的情况,再利用概率公式即可求得答案.
解答 解:列表得:
| 下端 上端 | ab | bc | ac |
| AB | AB,ab | AB,bc | AB,ac |
| BC | BC,ab | BC,bc | BC,ac |
| AC | AC,ab | AC,bc | AC,ac |
①上端连AB,下端连bc或ac;
②上端连BC,下端连ab或ac;
③上端连AB,下端连ab或bc.
∴这三根绳子能连结成一根长绳的概率P=$\frac{6}{9}$=$\frac{2}{3}$.
点评 考查了列表与树状图法求概率的知识,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$..

练习册系列答案
相关题目
19.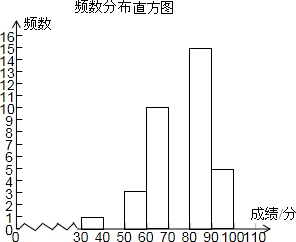 如图,某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.
如图,某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.
频数分布表
(1)以上分组的组距=10
(2)请补全频数分布表和频数分布直方图;
(3)请计算这50名同学的平均成绩;
(4)请你估计该校八年级期中考数学成绩优秀(不低于80分为优秀)的总人数.
 如图,某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.
如图,某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.频数分布表
| 成绩分组 | 频数 | 频率 |
| 30≤x<40 | 1 | 0.02 |
| 40≤x<50 | 1 | 0.02 |
| 50≤x<60 | 3 | 0.06 |
| 60≤x<70 | 10 | 0.2 |
| 70≤x<80 | 15 | 0.3 |
| 80≤x<90 | 15 | 0.3 |
| 90≤x<100 | 5 | 0.1 |
| 合计 | 50 | 1 |
(2)请补全频数分布表和频数分布直方图;
(3)请计算这50名同学的平均成绩;
(4)请你估计该校八年级期中考数学成绩优秀(不低于80分为优秀)的总人数.
16.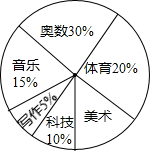 实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
(1)七年级共有学生360人;
(2)在表格中的空格处填上相应的数字;
(3)表格中所提供的六个数据的中位数是63;
(4)众数是72.
 实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.| 学习小组 | 体育 | 美术 | 科技 | 音乐 | 写作 | 奥数 |
| 人数 | 72 | 36 | 54 | 18 |
(2)在表格中的空格处填上相应的数字;
(3)表格中所提供的六个数据的中位数是63;
(4)众数是72.
14.如果$\frac{1}{a}$+$\frac{1}{b}$=1,则$\frac{a-2ab+b}{3a+2ab+3b}$的值为( )
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | -1 | D. | -3 |
 如图,在平面直角坐标中,过点A(4,0)的抛物线y=-x2+bx与直线y=-x+b交于另一点B.过抛物线y=-x2+bx的顶点E作EF⊥x轴于F点,点M(t,d)为抛物线y=-x2+bx在x轴上方的动点.
如图,在平面直角坐标中,过点A(4,0)的抛物线y=-x2+bx与直线y=-x+b交于另一点B.过抛物线y=-x2+bx的顶点E作EF⊥x轴于F点,点M(t,d)为抛物线y=-x2+bx在x轴上方的动点. 如图,已知:在△ABC中,D是边AB上的一点,且BC=BD,求证:∠ACB>∠A.
如图,已知:在△ABC中,D是边AB上的一点,且BC=BD,求证:∠ACB>∠A.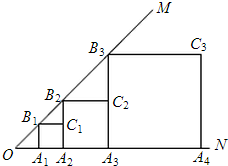 如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,周长记作L1;再作第二个正方形A2B2C2A3,周长记作L2;继续作第三个正方形A3B3C3A4,周长记作L3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第n个正方形的周长Ln=2n+1.
如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,周长记作L1;再作第二个正方形A2B2C2A3,周长记作L2;继续作第三个正方形A3B3C3A4,周长记作L3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第n个正方形的周长Ln=2n+1.