题目内容
7.若y=$\sqrt{x-2017}+\sqrt{2017-x}$+2016,则x-y=1.分析 直接利用二次根式有意义的条件得出x,y的值,进而得出答案.
解答 解:∵y=$\sqrt{x-2017}+\sqrt{2017-x}$+2016,
∴x=2017,y=2016,
则x-y=2017-2016=1.
故答案为:1.
点评 此题主要考查了二次根式有意义的条件,正确得出x,y的值是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.下列说法中正确的是( )
| A. | 3.14159是一个无理数 | B. | $\sqrt{0.25}$=±0.5 | ||
| C. | 若a为实数,则a2≥0 | D. | 16的平方根是4 |
12.下列方程或不等式变形正确的是( )
| A. | 方程-2x+6=8,移项得-2x=8+6 | |
| B. | 方程3+$\frac{8}{9}$x=6-3(x-1),去括号得:3+$\frac{8}{9}$x=6-3x-1 | |
| C. | 不等式$\frac{3x-1}{5}$-1>0,去分母得:3x-1-5>0 | |
| D. | 不等式-$\frac{1}{2}$x≥3,解得:x≥-6 |
17.点P(-3,7)到y轴的距离为( )
| A. | -3 | B. | 3 | C. | 7 | D. | -7 |
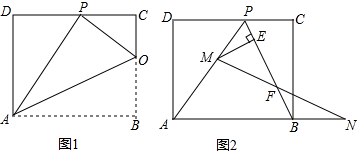
 写出推理理由:
写出推理理由: