题目内容
12. 已知,如图,直线l经过A(4,0)和B(0,4)两点,它与抛物线y=ax2在第一象限内相交于点P,又知△AOP的面积为$\frac{9}{2}$,求a的值.
已知,如图,直线l经过A(4,0)和B(0,4)两点,它与抛物线y=ax2在第一象限内相交于点P,又知△AOP的面积为$\frac{9}{2}$,求a的值.
分析 首先求得直线AB的解析式,然后根据面积求得P点的纵坐标,然后代入求得其横坐标,代入二次函数即可求解.
解答 解:设点P(x,y),直线AB的解析式为y=kx+b,
将A(4,0)、B(0,4)分别代入y=kx+b,
得k=-1,b=4,
故y=-x+4,
∵△AOP的面积为$\frac{9}{2}$=$\frac{1}{2}$×4×y
∴y=$\frac{9}{4}$,
再把Py=$\frac{9}{4}$代入y=-x+4,得x=$\frac{7}{4}$,
所以P($\frac{7}{4}$,$\frac{9}{4}$)
把P($\frac{7}{4}$,$\frac{9}{4}$)代入到y=ax2中得:$a=\frac{36}{49}$.
点评 本题考查的是三角形的性质以及二次函数与图象相结合的应用,难度中等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.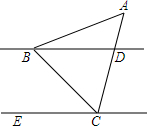 如图,在△ABC中,AB=AC,∠BAC=50°,点D在AC上,作直线BD,过C作CE∥BD,若∠BCE=40°,则∠ABD的度数是( )
如图,在△ABC中,AB=AC,∠BAC=50°,点D在AC上,作直线BD,过C作CE∥BD,若∠BCE=40°,则∠ABD的度数是( )
 如图,在△ABC中,AB=AC,∠BAC=50°,点D在AC上,作直线BD,过C作CE∥BD,若∠BCE=40°,则∠ABD的度数是( )
如图,在△ABC中,AB=AC,∠BAC=50°,点D在AC上,作直线BD,过C作CE∥BD,若∠BCE=40°,则∠ABD的度数是( )| A. | 10° | B. | 15° | C. | 25° | D. | 65° |
1.在如表所示的2003年1月份的日历中,用一个方框圈出任意3×3个数
(1)从左下角到右上角的三个数字之和为45,那么这9个数最中间的数是15
(2)假设最中间的数为x,则这9个数的和为9x.
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
(2)假设最中间的数为x,则这9个数的和为9x.
 标有1,1,2,3,3,5六个数字的立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为x,朝下一面的数为y,得到平面直角坐标系中的一个点(x,y).已知小华前二次掷得的两个点所确定的直线经过点P(0,-1),则他第三次掷得的点也在这条直线上的概率为$\frac{2}{3}$.
标有1,1,2,3,3,5六个数字的立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为x,朝下一面的数为y,得到平面直角坐标系中的一个点(x,y).已知小华前二次掷得的两个点所确定的直线经过点P(0,-1),则他第三次掷得的点也在这条直线上的概率为$\frac{2}{3}$.