题目内容
若线段ab满足（a2+4b2）：ab=4：1，求a：b的值．
考点：比例线段
专题：
分析：根据比例的性质得出a2+4b2=4ab，移项后变形，求出a=2b，即可求出答案．
解答：解：∵线段ab满足（a2+4b2）：ab=4：1，
∴a2+4b2=4ab，
∴a2-4ab+4b2=0，
∴（a-2b）2=0，
∴a-2b=0，
∴a=2b，
∴a：b=2b：b=2：1=2．
∴a2+4b2=4ab，
∴a2-4ab+4b2=0，
∴（a-2b）2=0，
∴a-2b=0，
∴a=2b，
∴a：b=2b：b=2：1=2．
点评：本题考查了比例的性质，平方根的应用，解此题的关键是求出a=2b．
练习册系列答案
小学课时特训系列答案
相关题目
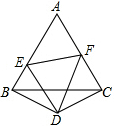如图，D是等边△ABC外的一点，DB=DC，∠BDC=120°，且E、F分别在AB和AC上．
如图，已知等边△ABC边长是6，BD=CE=2，BE与AD交于F，求AF的长．