题目内容
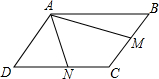 在平行四边形ABCD中,M,N分别是BC,DC的中点,AM=4,AN=3,且∠MAN=60°,求AB的长.
在平行四边形ABCD中,M,N分别是BC,DC的中点,AM=4,AN=3,且∠MAN=60°,求AB的长.考点:平行四边形的性质
专题:几何图形问题,数形结合,分类讨论
分析:首先延长DC和AM交于E,过点E作EH⊥AN于点H,易证得△ABM≌△ECM,即可得AB=
NE,然后由AM=4,AN=3,且∠MAN=60°,求得AH,NH与EH的长,继而求得EN的长,则可求得答案.
| 2 |
| 3 |
解答: 解:延长DC和AM交于E,过点E作EH⊥AN于点H,
解:延长DC和AM交于E,过点E作EH⊥AN于点H,
∵四边形ABCD为平行四边形
∴AB∥CE,
∴∠BAM=∠E,∠B=∠ECM,
∵M为BC的中点,
∴BM=CM,
在△ABM和△ECM中,
,
∴△ABM≌△ECM(AAS),
∴AB=CD=CE,AM=EM=4,
∵N为边DC的中点,
∴NE=3NC=
AB 即AB=
NE,
∵AN=3,AE=2AM=8,且∠MAN=60°,
∴∠AEH=30°,
∴AH=
AE=4,
∴EH=
=4
,
∴NH=AH-AN=4-3=1,
∴EN=
=7,
∴AB=
×7=
.
 解:延长DC和AM交于E,过点E作EH⊥AN于点H,
解:延长DC和AM交于E,过点E作EH⊥AN于点H,∵四边形ABCD为平行四边形
∴AB∥CE,
∴∠BAM=∠E,∠B=∠ECM,
∵M为BC的中点,
∴BM=CM,
在△ABM和△ECM中,
|
∴△ABM≌△ECM(AAS),
∴AB=CD=CE,AM=EM=4,
∵N为边DC的中点,
∴NE=3NC=
| 3 |
| 2 |
| 2 |
| 3 |
∵AN=3,AE=2AM=8,且∠MAN=60°,
∴∠AEH=30°,
∴AH=
| 1 |
| 2 |
∴EH=
| AE2-AH2 |
| 3 |
∴NH=AH-AN=4-3=1,
∴EN=
| NH2+EH2 |
∴AB=
| 2 |
| 3 |
| 14 |
| 3 |
点评:此题考查了平行四边形的性质、全等三角形的判定与性质以及勾股定理.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
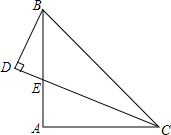 已知,如图△ABC中,AB=AC,∠A=90°,∠ACB的平分线CD交AB于点E,∠BDC=90°,求证:CE=2BD.
已知,如图△ABC中,AB=AC,∠A=90°,∠ACB的平分线CD交AB于点E,∠BDC=90°,求证:CE=2BD.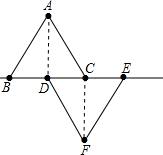 在直角坐标中,有两个边长都为10cm的等边三角形△ABC和△DEF,且BC、DE与x轴重合,B与原点O重合,连结AD、CF.
在直角坐标中,有两个边长都为10cm的等边三角形△ABC和△DEF,且BC、DE与x轴重合,B与原点O重合,连结AD、CF.
