题目内容
如图,在四边形ABCD中,AC⊥BD,BD=12,AC=16,E,F分别为AB,CD的中点,求EF的长.


考点:三角形中位线定理,勾股定理
专题:计算题
分析:如图,取BC边的中点G,连接EG、FG.根据三角形中位线定理易求EG、FG的长度,并且∠EGF=90°,所以在直角△EGF中,利用勾股定理来求EF的长度.
解答: 解:如图,取BC边的中点G,连接EG、FG.
解:如图,取BC边的中点G,连接EG、FG.
∵E,F分别为AB,CD的中点,
∴EG是△ABC的中位线,FG是△BCD的中位线,
∴EG
AC,FG
BD.
又BD=12,AC=16,AC⊥BD,
∴EG=8,FG=6,EG⊥FG,
∴在直角△EGF中,由用勾股定理,得
EF=
=
=10,即EF的长度是10.
 解:如图,取BC边的中点G,连接EG、FG.
解:如图,取BC边的中点G,连接EG、FG.∵E,F分别为AB,CD的中点,
∴EG是△ABC的中位线,FG是△BCD的中位线,
∴EG
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
又BD=12,AC=16,AC⊥BD,
∴EG=8,FG=6,EG⊥FG,
∴在直角△EGF中,由用勾股定理,得
EF=
| EG2+FG2 |
| 82+62 |
点评:本题考查了三角形中位线定理、勾股定理.根据已知条件推知△EGF是直角三角形是解题的关键.

练习册系列答案
相关题目
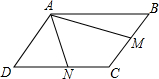 在平行四边形ABCD中,M,N分别是BC,DC的中点,AM=4,AN=3,且∠MAN=60°,求AB的长.
在平行四边形ABCD中,M,N分别是BC,DC的中点,AM=4,AN=3,且∠MAN=60°,求AB的长.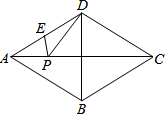 已知四边形ABCD为菱形,∠BAD=60°,E为AD中点,AB=6cm,P为AC上任一点.求PE+PD的最小值是
已知四边形ABCD为菱形,∠BAD=60°,E为AD中点,AB=6cm,P为AC上任一点.求PE+PD的最小值是