题目内容
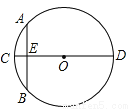
“圆材埋壁”是我国古代著名的数学著作《九章算数》中的一个问题,”今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何? 用现在的数学语言表述是:如图,CD为⊙O的直径,弦AB⊥CD垂足为E,CE=1寸,AB=10寸,求直径CD的长”.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
“圆材埋壁”是我国古代著名的数学著作《九章算数》中的一个问题,”今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何? 用现在的数学语言表述是:如图,CD为⊙O的直径,弦AB⊥CD垂足为E,CE=1寸,AB=10寸,求直径CD的长”.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案