Question

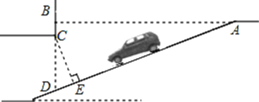
【题目】如图，△ABC中，∠BAC＝45°，∠ABC＝60°，AB＝4，D是边BC上的一个动点，以AD为直径画⊙O分别交AB、AC于点E、F，则弦EF长度的最小值为（ ）

A.B.C.2D.2

Answer 1

【答案】B

【解析】

作AH⊥BC于H，OG⊥EF于G，连接OE、OF，如图，利用圆周角定理得∠EOF=120°，利用含30度的直角三角形三边的关系得到EF=2EG=OE，所以当⊙O的半径最小时，EF的值最小，此时AD最小，AD的最小值为AH的长，然后计算出AH的长就可得到EF的最小值．

作AH⊥BC于H，OG⊥EF于G，连接OE、OF，如图，

∵∠EOF＝2∠EAF＝2×60°＝120°，OE＝OF，

∴∠OEF＝30°，

∴OG＝OE，

∴EG＝OG，

∵OG⊥EF，

∴EG＝FG＝OE，

∴EF＝2EG＝OE，

当OE的值最小时，EF的值最小，

此时AD最小，AD的最小值为AH的长，

在Rt△ABH中，∵∠ABH＝45°，

∴AH＝AB＝2，

∴OE的最小值为，

∴EF的最小值为×＝．

故选：B．