题目内容
17.已知四边形ABCD的两条对角线AC与BD互相垂直,则下列结论正确的是( )| A. | 当AC=BD时,四边形ABCD是矩形 | |
| B. | 当AB=AD,CB=CD时,四边形ABCD是菱形 | |
| C. | 当AC=BD,AD=AB时,四边形ABCD是正方形 | |
| D. | 当AB=AD=BC时,四边形ABCD是菱形 |
分析 根据条件首先能否判定为平行四边形,是平行四边形的才有可能是矩形、菱形或正方形,否则不正确.
解答 解:A:由对角线AC与BD互相垂直,当AC=BD时,不能判定四边形ABCD是平行四边形,那么不一定是矩形;故A不正确;
B:对角线AC与BD互相垂直,当AB=AD,CB=CD时,不能判定四边形ABCD是平行四边形,那么不一定是菱形;故B不正确;
C:对角线AC与BD互相垂直,当AC=BD,AD=AB时,不能判定四边形ABCD是平行四边形,那么不一定是正方形;故C不正确;
D:对角线AC与BD互相垂直,当AB=AD=BC时,能证出对角线互相平分,∴四边形ABCD是平行四边形,再根据对角线互相垂直的平行四边形是菱形,故D正确.
故选:D.
点评 本题考查了平行四边形的判定、菱形的判定、矩形的判定以及正方形的判定;熟练掌握平行四边形的判定方法和与矩形、菱形、正方形的关系是解题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
5.为了美化城市,建设中的某休闲广场准备用边长相同的正三角形与正方形两种地转镶嵌地面,在每一个顶点的周围,正三角形、正方形地转的个数分别是( )
| A. | 3,2 | B. | 2,3 | C. | 4,1 | D. | 2、2 |
6.若计算(x-5)(x+a)的结果是x2-bx-10,则a的值是( )
| A. | -2 | B. | 2 | C. | 3 | D. | -3 |
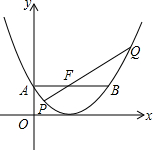 如图,已知抛物线C1:y1=$\frac{1}{4}$x2-x+1,点F(2,1).
如图,已知抛物线C1:y1=$\frac{1}{4}$x2-x+1,点F(2,1). 如图,?ABCD中,AE∥CF,AE与BC相交于点P,CF与BD相交于点Q,BP与DQ是否相等,请说明理由.
如图,?ABCD中,AE∥CF,AE与BC相交于点P,CF与BD相交于点Q,BP与DQ是否相等,请说明理由.