题目内容
4.△ABC中,∠A=90°,点D在线段BC上(端点B除外),∠EDB=$\frac{1}{2}$∠C,BE⊥DE于点E,DE与AB相交于点F,过F作FM∥AC交BD于M.
(1)当AB=AC时(如图1),求证:①FM=MD;②FD=2BE;
(2)当AB=kAC时(k>0,如图2),用含k的式子表示线段FD与BE之间的数量关系,并说明理由.
分析 (1)①利用等腰直角三角形得出结合平行线的性质得出∠DMF=∠MFD,进而得出答案;
②根据题意证明△BEF∽△DEB,然后利用相似三角形的性质,得到BE与FD的数量关系;
(2)首先证明△GBN∽△FDN,利用三角形相似的性质得到BE与FD的数量关系.
解答 (1)证明:①如图1,∵AB=AC,∠A=90°
∴∠ABC=∠C=45°
∵∠EDB=$\frac{1}{2}$∠C
∴∠EDB=22.5°
∵FM∥AC,
∴∠FMB=45°,
∴∠MFD=22.5°,
∴∠DMF=∠MFD,
∴MF=MD;
②在△BEF和△DEB中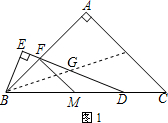
∵∠E=∠E=90°
∠EBF=∠EDB=22.5°
∴△BEF∽△DEB
如图1:作BG平分∠ABC,交DE于G点,
∴BG=GD,△BEG是等腰直角三角形
设EF=x,BE=y,
则:BG=GD=$\sqrt{2}$y,
FD=$\sqrt{2}$y+y-x,
∵△BEF∽△DEB
∴$\frac{x}{y}$=$\frac{y}{y+\sqrt{2}y}$,
得:x=($\sqrt{2}$-1)y,
∴FD=2BE;
(2)解:过点D作DG∥AC,交BE的延长线于点G,与BA交于点N,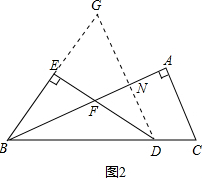
∵DG∥AC,
∴∠GDB=∠C,
∵∠EDB=$\frac{1}{2}$∠C,
∴∠EDB=∠GDE,
∵BE⊥DE,
∴∠BED=∠DEG,
在△DEG和△DEB中
$\left\{\begin{array}{l}{∠EDG=∠EDB}\\{DE=DE}\\{∠GED=∠BED}\end{array}\right.$,
∴△DEG≌△DEB(ASA),
∴BE=$\frac{1}{2}$GB,∠BND=∠GNB=90°,∠EBF=∠NDF,
∴△GBN∽△FDN,
∴$\frac{GB}{FD}$=$\frac{NB}{ND}$,即$\frac{BE}{FD}$=$\frac{BN}{2DN}$,
又∵DG∥AC,
∴△BND∽△BAC,
∴$\frac{BN}{AB}$=$\frac{DN}{AC}$,
即$\frac{BN}{DN}$=$\frac{AB}{AC}$=k,
∴$\frac{BE}{FD}$=$\frac{k}{2}$,
∴FD=$\frac{2}{k}$BE.
点评 本题考查的是相似三角形的判定与性质,(1)利用等腰直角三角形的性质进行判定和计算.(2)结合图形利用三角函数和相似三角形进行计算求出线段间的关系.

 综合自测系列答案
综合自测系列答案| A. | 2$\sqrt{5}$×$\sqrt{5}$ | B. | 2$\sqrt{3}$×$3\sqrt{2}$ | C. | ($\sqrt{3}$+$\sqrt{2}$)×$[-(\sqrt{3}+\sqrt{2})]$ | D. | $\sqrt{3a-4b}•\sqrt{3a+4b}$ |
 如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A,B间的距离.有关他这次探究活动的描述错误的是( )
如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A,B间的距离.有关他这次探究活动的描述错误的是( )| A. | S△CMN=$\frac{1}{2}$S△ABC | B. | CM:CA=1:2 | C. | MN∥AB | D. | AB=24m |

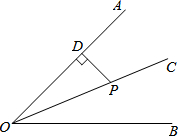 如图,OC是∠AOB的平分线,PD⊥DA,垂足为D,PD=2,则点P到OB的距离是2.
如图,OC是∠AOB的平分线,PD⊥DA,垂足为D,PD=2,则点P到OB的距离是2.