题目内容
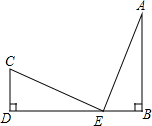 如图,CD⊥DB于D,AB⊥DB于B,CD=EB,AB=ED.求证:
如图,CD⊥DB于D,AB⊥DB于B,CD=EB,AB=ED.求证:(1)△CDE≌△EBA;
(2)CE⊥AE.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)易证∠B=∠D=90°,即可证明△CDE≌△EBA,即可解题;
(2)由(1)结论可得∠C=∠AEB,根据∠C+∠CED=90°,即可解题.
(2)由(1)结论可得∠C=∠AEB,根据∠C+∠CED=90°,即可解题.
解答:证明:(1)∵CD⊥DB于D,AB⊥DB于B,
∴∠B=∠D=90°,
在△CDE和△EBA中,
,
∴△CDE≌△EBA(SAS);
(2)∵△CDE≌△EBA,
∴∠C=∠AEB,
∵∠C+∠CED=90°,
∴∠AEB+∠CED=90°,
∴∠AEC=90°,
∴CE⊥AE,
∴∠B=∠D=90°,
在△CDE和△EBA中,
|
∴△CDE≌△EBA(SAS);
(2)∵△CDE≌△EBA,
∴∠C=∠AEB,
∵∠C+∠CED=90°,
∴∠AEB+∠CED=90°,
∴∠AEC=90°,
∴CE⊥AE,
点评:本题考查了全等三角形的判定,考查了全等三角形对角边相等的性质,本题中求证△CDE≌△EBA是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
将抛物线y=3x2平移得到抛物线y=3(x-4)2-1的步骤是( )
| A、向左平移4个单位,再向上平移1个单位 |
| B、向左平移4个单位,再向下平移1个单位 |
| C、向右平移4个单位,再向上平移1个单位 |
| D、向右平移4个单位,再向下平移1个单位 |
 如图,在数轴上有两点A,B,它们所对应的数分别是a,8,(a<8),把线段AB的中点记为点C.
如图,在数轴上有两点A,B,它们所对应的数分别是a,8,(a<8),把线段AB的中点记为点C. 如图,AB为⊙O的一条弦,CD为直径(C不与A、B及
如图,AB为⊙O的一条弦,CD为直径(C不与A、B及
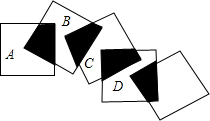 将5个边长都为1cm的正方形按如图所示的样子摆放,点A.B.C.D分别是四个正方形的中心,则图中四块阴影部分的面积的和为
将5个边长都为1cm的正方形按如图所示的样子摆放,点A.B.C.D分别是四个正方形的中心,则图中四块阴影部分的面积的和为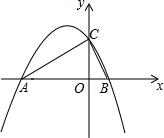 如图所示,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C(0,2),若∠ACB=90°,BC=
如图所示,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C(0,2),若∠ACB=90°,BC=