题目内容
找规律:
(1)等差型:3,8,13,18,23, ,…用n表示为 ;
(2)等比型:3,6,12,24,48, ,…用n表示为 ;
(3)指数型:1,4,9,16,25,36, ,…用n表示为 ;
0,3,8,15,24,35, ,…用n表示为 ;
(4)和差型:3,5,8,13,21, ;
-1,1,2,1,-1,-2,-1, .
(1)等差型:3,8,13,18,23,
(2)等比型:3,6,12,24,48,
(3)指数型:1,4,9,16,25,36,
0,3,8,15,24,35,
(4)和差型:3,5,8,13,21,
-1,1,2,1,-1,-2,-1,
考点:规律型:数字的变化类
专题:
分析:(1)根据后一个数比前一个数大5解答;
(2)根据后一个数是前一个数的2倍解答;
(3)数列为从1开始的连续自然数的平方;为上一列数相应的数减去1;
(4)第一行数的后一个数为前面两个数的和;第二行数的后一个数是前面两个数的差.
(2)根据后一个数是前一个数的2倍解答;
(3)数列为从1开始的连续自然数的平方;为上一列数相应的数减去1;
(4)第一行数的后一个数为前面两个数的和;第二行数的后一个数是前面两个数的差.
解答:解:(1)(1)等差型:3,8,13,18,23,28,…用n表示为5n-2;
(2)等比型:3,6,12,24,48,96,…用n表示为3•2n-1;
(3)指数型:1,4,9,16,25,36,49,…用n表示为n2;
0,3,8,15,24,35,48,…用n表示为n2-1;
(4)和差型:3,5,8,13,21,34;
-1,1,2,1,-1,-2,-1,1.
故答案为:(1)28,5n-2;(2)96,3•2n-1;(3)49,n2,48,n2-1;(4)34,1.
(2)等比型:3,6,12,24,48,96,…用n表示为3•2n-1;
(3)指数型:1,4,9,16,25,36,49,…用n表示为n2;
0,3,8,15,24,35,48,…用n表示为n2-1;
(4)和差型:3,5,8,13,21,34;
-1,1,2,1,-1,-2,-1,1.
故答案为:(1)28,5n-2;(2)96,3•2n-1;(3)49,n2,48,n2-1;(4)34,1.
点评:本题是对数字变化规律的考查,此类题目仔细观察相邻数的关系是解题的关键,本题难点在于(4)的第二行观察出后一个数是前面两个数的差.

练习册系列答案
相关题目
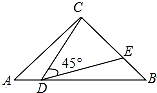 如图,△ABC中,∠ACB=90°,AC=BC=2,点D在线段AB上运动(不包括端点),∠CDE=45°,DE与CB交于点E,若DB=x,CE=y.
如图,△ABC中,∠ACB=90°,AC=BC=2,点D在线段AB上运动(不包括端点),∠CDE=45°,DE与CB交于点E,若DB=x,CE=y.
 如图,将一块直角三角形的直角顶点放在C(1,
如图,将一块直角三角形的直角顶点放在C(1,