题目内容
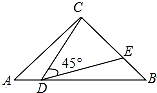 如图,△ABC中,∠ACB=90°,AC=BC=2,点D在线段AB上运动(不包括端点),∠CDE=45°,DE与CB交于点E,若DB=x,CE=y.
如图,△ABC中,∠ACB=90°,AC=BC=2,点D在线段AB上运动(不包括端点),∠CDE=45°,DE与CB交于点E,若DB=x,CE=y.(1)试说明:△ACD∽△BDE;
(2)用含有x的代数式表示y;
(3)当△CDE是等腰三角形时,求AD的长.
考点:相似三角形的判定与性质
专题:
分析:(1)根据三角形内角和定理以及邻补角的定义证明∠DEB=∠ADC,然后根据∠A=∠B即可证得两个三角形相似;
(2)根据相似三角形的对应边的比相等即可求解;
(3)分CD=DE、CD=CE、CE=DE三种情况进行讨论即可求解.
(2)根据相似三角形的对应边的比相等即可求解;
(3)分CD=DE、CD=CE、CE=DE三种情况进行讨论即可求解.
解答:解:(1)∵△ABC中,∠ACB=90°,AC=BC=2,
∴∠A=∠B=45°,AB=2
.
∵△BDE中,∠DEB=180°-∠EDB-∠B=180°-∠EDB-45°=135°-∠EDB,
又∵∠ADC=180°-∠CDE-∠EDB=135°-∠EDB,
∴∠DEB=∠ADC,
又∵∠A=∠B,
∴△ACD∽△BDE;
(2)若DB=x,CE=y,AD=2
-x,BE=BC-CE=2-y.
∵△ACD∽△BDE,
∴
=
,即
=
,
∴y=
x2-
x+2;
(3)当CD=DE时,
∵△ACD∽△BDE,
∴△ACD≌△BDE,
∴AC=BD=2,
则AD=AB-BD=2
-2;
当CD=CE时,∠CDE=∠CED>∠B=45°,则此时一定不成立;
当CE=DE时,∠CDA=∠DCE=45°,则CD是∠ACB的平分线,则AD=
AB=
.
故答案是:2
-2或
.
∴∠A=∠B=45°,AB=2
| 2 |
∵△BDE中,∠DEB=180°-∠EDB-∠B=180°-∠EDB-45°=135°-∠EDB,
又∵∠ADC=180°-∠CDE-∠EDB=135°-∠EDB,
∴∠DEB=∠ADC,
又∵∠A=∠B,
∴△ACD∽△BDE;
(2)若DB=x,CE=y,AD=2
| 2 |

∵△ACD∽△BDE,
∴
| AC |
| BD |
| AD |
| BE |
| 2 |
| x |
2
| ||
| 2-y |
∴y=
| 1 |
| 2 |
| 2 |
(3)当CD=DE时,
∵△ACD∽△BDE,
∴△ACD≌△BDE,
∴AC=BD=2,
则AD=AB-BD=2
| 2 |
当CD=CE时,∠CDE=∠CED>∠B=45°,则此时一定不成立;
当CE=DE时,∠CDA=∠DCE=45°,则CD是∠ACB的平分线,则AD=
| 1 |
| 2 |
| 2 |
故答案是:2
| 2 |
| 2 |
点评:本题考查了等腰三角形的判定与性质以及相似三角新的判定与性质,正确证明∠DEB=∠ADC是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
计算3.14×5.5966+3.14×(-8.5966)的值为( )
| A、9.42 |
| B、-9.42 |
| C、37.68 |
| D、-37.68 |
方程(x-2)2=3(x-2)的解为( )
| A、x=2 |
| B、x=5 |
| C、x1=2,x2=5 |
| D、x1=2,x2=3 |
下列函数中,是二次函数的是( )
A、y=x2-
| ||
| B、y=2x2+3x | ||
| C、y=-x2+y2 | ||
| D、y=x+1 |
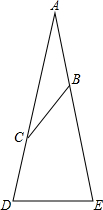 如图,在△ABC中,已知:AB=BC=CD=DE,∠A=20°,求∠E的度数.
如图,在△ABC中,已知:AB=BC=CD=DE,∠A=20°,求∠E的度数. 如图,△ABC的一边AB为⊙O的直径,AC是⊙O的切线,且AB=AC,则∠C=
如图,△ABC的一边AB为⊙O的直径,AC是⊙O的切线,且AB=AC,则∠C=