Question

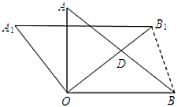
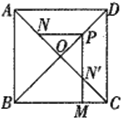
【题目】如图，在正方形中，点分别在和上，.

(1)求证：.

(2)连接交于点，延长至点，使，连接，.求证：四边形是菱形.

Answer 1

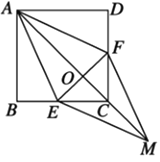
【答案】(1)证明见解析；(2)证明见解析.

【解析】

（1）根据正方形的性质可得AB=AD，∠B=∠D=90°，然后利用“SAS”证明Rt△ABE和Rt△ADF全等，根据全等三角形对应边相等可得BE=DF；

（2）求出CE=CF，然后利用“边边边”证明△AEC和△AFC全等，根据全等三角形对应角相等可得∠EAC=∠FAC，再根据等腰三角形三线合一的性质可得AC垂直平分EF，根据线段垂直平分线上的点到两端点的距离相等可得EM=FM，再判断出EF垂直平分AM，根据线段垂直平分线上的点到两端点的距离相等可得AE=EM，然后根据四条边都相等的四边形是菱形证明．

证明：(1)在正方形中，

，

在和中，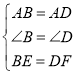

(全等三角形的对应边相等)

(2)，

，即

在和中，

又

垂直平分(等腰三角形三线合一)

又

四边形是平行四边形(对角线互相平分的四边形是平行四边形)

四边形是菱形(对角线互相垂直的平行四边形是菱形)